Beams Supported at Both Ends with Continuous and Point Loads: Stress, Deflection, Formulas and Calculators

The bending stress in a bending beam can be expressed as

σ = y M / I                                     (1)

where

σ = bending stress (Pa (N/m²), N/mm², psi)

y = distance to point from neutral axis (m, mm, in)

M = bending moment (Nm, lb in)

I = moment of Inertia (m⁴, mm⁴, in⁴)

• Beams - Supported at Both Ends - Continuous and Point Loads
• Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
• Beams - Fixed at Both Ends - Continuous and Point Loads

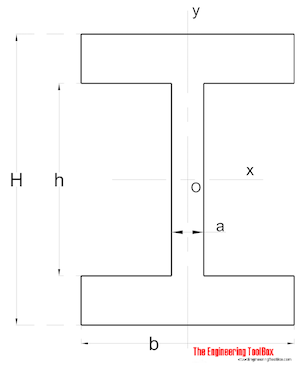
Distance y in a typical steel beam profile.

The calculator below can be used to calculate maximum stress and deflection of beams with one single or uniform distributed loads.

Beam Supported at Both Ends - Uniform Continuous Distributed Load

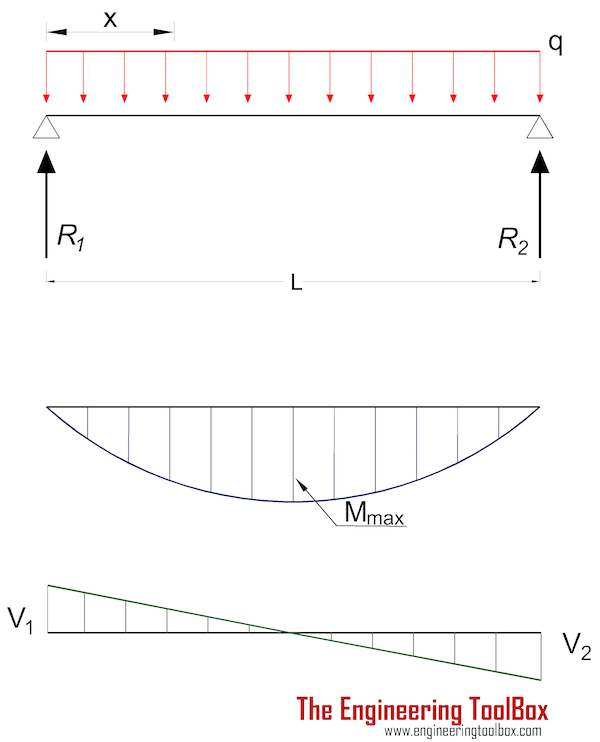
The moment in a beam with uniform load supported at both ends in position x can be expressed as

M_x = q x (L - x) / 2                                          (2)

where

M_x = moment in position x (Nm, lb in)

x = distance from end (m, mm, in)

The maximum moment is at the center of the beam at distance L/2 and can be expressed as

M_max = q L² / 8                                          (2a)

where

M_max = maximum moment (Nm, lb in)

q = uniform load per length unit of beam (N/m, N/mm, lb/in)

L = length of beam (m, mm, in)

Maximum Stress

Equation 1 and 2a can be combined to express maximum stress in a beam with uniform load supported at both ends at distance L/2 as

σ_max = y_max q L² / (8 I)                                     (2b)

where

σ_max = maximum stress (Pa (N/m²), N/mm², psi)

y_max = distance to extreme point from neutral axis (m, mm, in)

• 1 N/m²= 1×10^-6 N/mm² = 1 Pa = 1.4504×10^-4 psi
• 1 psi (lb/in²) = 144 psf (lb_f/ft²) = 6,894.8 Pa (N/m²) = 6.895×10^-3 N/mm²

• Ulimate tensile strength for some common materials

Maximum deflection :

δ_max = 5 q L⁴ / (384 E I)                                     (2c)

where

δ_max = maximum deflection (m, mm, in)

E = Modulus of Elasticity (Pa (N/m²), N/mm², psi)

Deflection in position x:

δ_x = q x (L³ - 2 L x²+ x³) / (24 E I)                                     (2d)

Note! - deflection is often the limiting factor in beam design. For some applications beams must be stronger than required by maximum loads, to avoid unacceptable deflections.

Forces acting on the ends:

R₁ = R₂

= q L / 2                                      (2e)

where

R = reaction force (N, lb)

Example - Beam with Uniform Load, Metric Units

A UB 305 x 127 x 42 beam with length 5000 mm carries a uniform load of 6 N/mm . The moment of inertia for the beam is 8196 cm⁴ (81960000 mm⁴) and the modulus of elasticity for the steel used in the beam is 200 GPa (200000 N/mm²) . The height of the beam is 300 mm (the distance of the extreme point to the neutral axis is 150 mm ).

The maximum stress in the beam can be calculated

σ_max = (150 mm) (6 N/mm) (5000 mm)²/ (8 (81960000 mm⁴))

= 34.3 N/mm²

= 34.3 10⁶ N/m²(Pa)

= 34.3 MPa

The maximum deflection in the beam can be calculated

δ_max = 5 (6 N/mm) (5000 mm)⁴/ ((200000 N/mm²) (81960000 mm⁴) 384)

= 2.98 mm

Uniform Load Beam Calculator - Metric Units

q - Uniform load (N/mm)

L - Length of Beam (mm)

I - Moment of Inertia (mm⁴)

E - Modulus of Elasticity (N/mm²)

y - Distance of extreme point off neutral axis (mm)

• 1 mm⁴ = 10^-4 cm⁴ = 10^-12 m⁴
• 1 cm⁴ = 10^-8 m = 10⁴ mm
• 1 in⁴ = 4.16×10⁵ mm⁴ = 41.6 cm⁴
• 1 N/mm² = 10⁶ N/m²(Pa)

Uniform Load Beam Calculator - Imperial Units

q - Load (lb/in)

L - Length of Beam (in)

I - Moment of Inertia (in⁴)

E - Modulus of Elasticity (psi)

y - Distance of extreme point off neutral axis (in)

Example - Beam with Uniform Load, Imperial Units

The maximum stress in a "W 12 x 35" Steel Wide Flange beam, 100 inches long, moment of inertia 285 in⁴ , modulus of elasticity 29000000 psi , with uniform load 100 lb/in can be calculated as

σ_max = y_max q L² / (8 I)

= (6.25 in) (100 lb/in) (100 in)²/ (8 (285 in⁴))

= 2741 (lb/in², psi)

The maximum deflection can be calculated as

δ_max = 5 q L⁴ / (E I 384)

= 5 (100 lb/in) (100 in)⁴/ ((29000000 lb/in²) (285 in⁴) 384)

= 0.016 in

Beam Supported at Both Ends - Load at Center

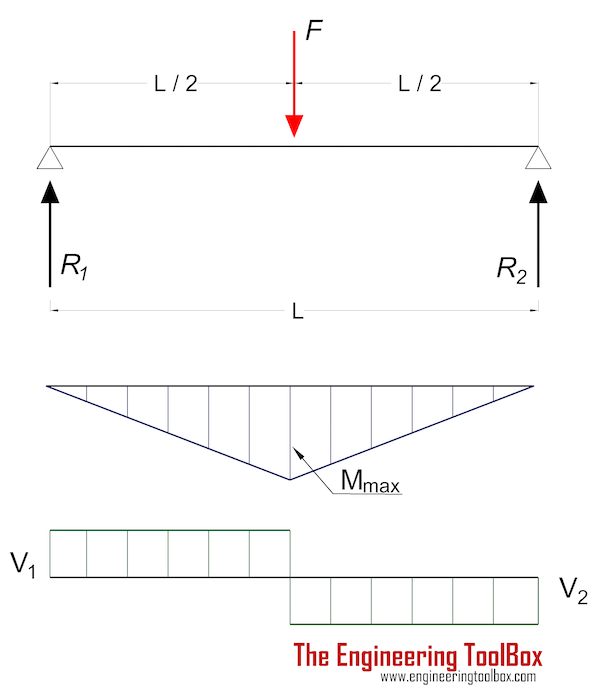
Maximum moment in a beam with center load supported at both ends:

M_max = F L / 4                                          (3a)

Maximum Stress

Maximum stress in a beam with single center load supported at both ends:

σ_max = y_max F L / (4 I)                                    (3b)

where

F = load (N, lb)

Maximum deflection can be expressed as

δ_max = F L³ / (48 E I)                                  (3c)

Forces acting on the ends:

R₁ = R₂

= F / 2                                      (3d)

Single Center Load Beam Calculator - Metric Units

F - Load (N)

L - Length of Beam (mm)

I - Moment of Inertia (mm⁴)

E - Modulus of Elasticity (N/mm²)

y - Distance of extreme point off neutral axis (mm)

Single Center Load Beam Calculator - Imperial Units

F - Load (lb)

L - Length of Beam (in)

I - Moment of Inertia (in⁴)

E - Modulus of Elasticity (psi)

y - Distance of extreme point off neutral axis (in)

Example - Beam with a Single Center Load

The maximum stress in a "W 12 x 35" Steel Wide Flange beam, 100 inches long, moment of inertia 285 in⁴ , modulus of elasticity 29000000 psi , with a center load 10000 lb can be calculated like

σ_max = y_max F L / (4 I)

= (6.25 in) (10000 lb) (100 in) / (4 (285 in⁴))

= 5482 (lb/in², psi)

The maximum deflection can be calculated as

δ_max = F L³ / E I 48

= (10000 lb) (100 in)³/ ((29000000 lb/in²) (285 in⁴) 48)

= 0.025 in

Some Typical Vertical Deflection Limits

• total deflection : span/250
• live load deflection : span/360
• cantilevers : span/180
• domestic timber floor joists : span/330 (max 14 mm)
• brittle elements : span/500
• crane girders : span/600

Beam Supported at Both Ends - Eccentric Load

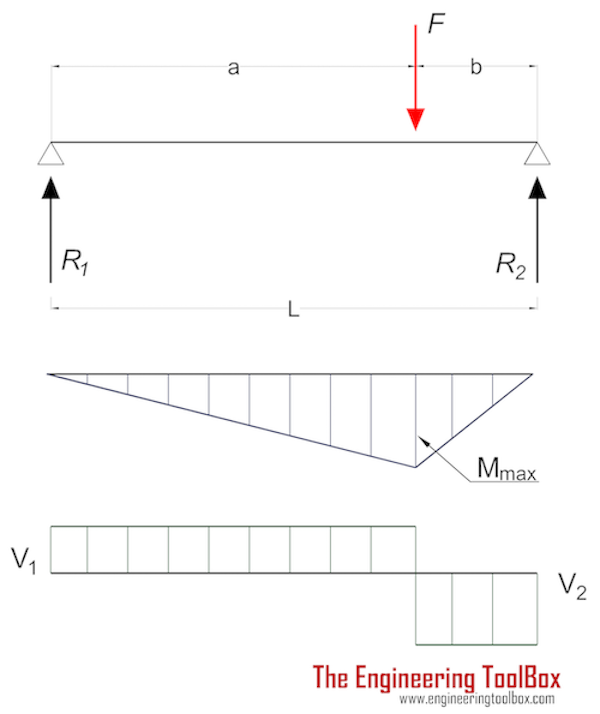
Maximum moment in a beam with single eccentric load at point of load:

M_max = F a b / L                                          (4a)

Maximum Stress

Maximum stress in a beam with single center load supported at both ends:

σ_max = y_max F a b / (L I)                                    (4b)

Maximum deflection at point of load can be expressed as

δ_F = F a² b² / (3 E I L)                                  (4c)

Forces acting on the ends:

R₁ = F b / L                                 (4d)

R₂= F a / L                                 (4e)

Beam Supported at Both Ends - Two Eccentric Loads

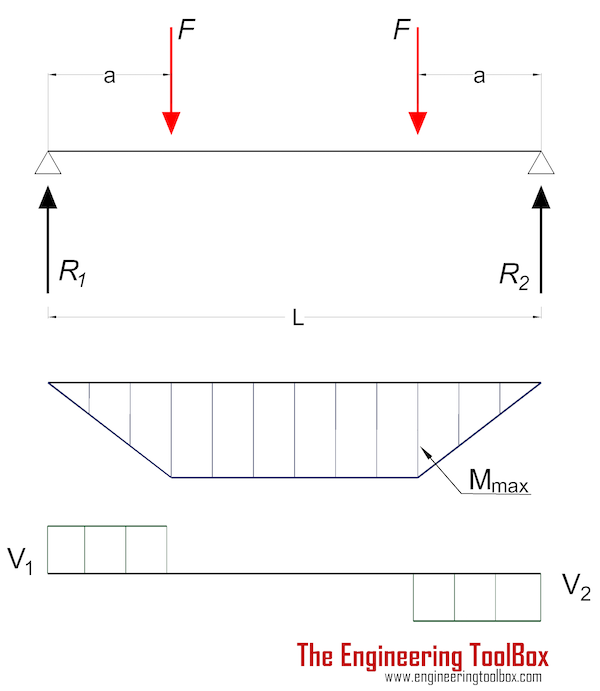
Maximum moment (between loads) in a beam with two eccentric loads:

M_max = F a                                          (5a)

Maximum Stress

Maximum stress in a beam with two eccentric loads supported at both ends:

σ_max = y_max F a / I                                    (5b)

Maximum deflection at point of load can be expressed as

δ_F = F a (3L²- 4 a²) / (24 E I)                                  (5c)

Forces acting on the ends:

R₁ = R₂

= F                                  (5d)

Insert beams to your Sketchup model with the Engineering ToolBox Sketchup Extension

Beam Supported at Both Ends - Three Point Loads

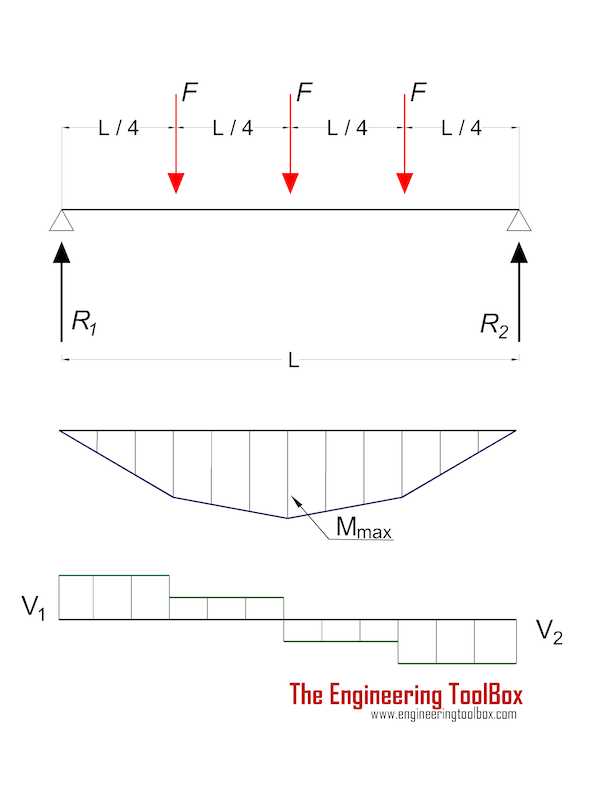
Maximum moment (between loads) in a beam with three point loads:

M_max = F L / 2                                          (6a)

Maximum Stress

Maximum stress in a beam with three point loads supported at both ends:

σ_max = y_max F L / (2 I)                                    (6b)

Maximum deflection at the center of the beam can be expressed as

δ_F = F L³/ (20.22 E I)                               (6c)

Forces acting on the ends:

R₁ = R₂

= 1.5 F                                  (6d)