Weight of Beams - Stress and Strain
Stress and deformation of vertical beams due to own weight.
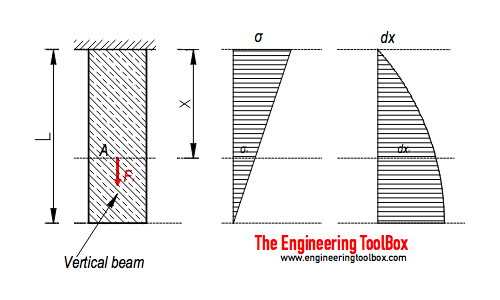
Axial Force
The axial force acting in a cross sectional area in distance x in a vertical beam due to it's own weight - can be calculated as
Fx = γ A (L - x) (1)
where
Fx = axial force in distance x (N)
y = specific weight - unit volume weight (N/m3)
A = cross-sectional area (m2)
L = length of beam (m)
x = distance (m)
The specific weight can be expressed as
y = ρ g (2)
where
ρ = density of beam (kg/m3)
g = acceleration of gravity (9.81 m/s2)
(1) can with (2) be modified to
Fx = ρ g A (L - x) (2b)
Axial Stress
The axial stress at a distance x can be calculated as
σx = Fx / A
= γ (L - x)
= ρ g (L - x) (3)
where
σx = axial stress (Pa, N/m2)
Note! - the cross-sectional area is irrelevant.
The axial stress at distance x = L
σx=L = γ (L - L)
= ρ g (L - L)
= 0 (3a)
The axial stress at distance x = 0
σx=0 = γ (L - 0)
= ρ g (L - 0)
= γ L
= ρ g L (3b)
Axial Deformation
The axial deformation at distance x can be calculated as
dxx = y x (2 L - x) / (2 E)
= ρ g x (2 L - x) / (2 E) (4)
where
dx = deformation (m)
E = modulus of elasticity (N/m2)
The axial deformation at distance x = L
dxx=L = y L2 / (2 E)
= ρ g L2 / (2 E) (4a)
The axial deformation at distance x = 0
dxx=0 = 0 (4b)
Example - Stress and Axial Deformation of a Vertical Steel Rod
A 45 m long steel rod with density 7280 kg/m3 and cross-sectional area 0.1 m2 is mounted as indicated in the figure above.
The maximum force acting in the rod at distance x = 0 m can be calculated with (1b)
Fx=0 = (7280 kg/m3) (9.81 m/s2) (0.1 m2) ((45 m) - (0 m))
= 321376 N
= 321 kN
The maximum axial stress in the rod at distance x = 0 m can be calculated (3b)
σx=0 = (7280 kg/m3) (9.81 m/s2) (45 m)
= 3213756 N/m2(Pa)
= 3.2 MPa
The modulus of elasticity for the steel rod is 200 GPa (200×109 N/m2). The axial deformation at distance x = 45 m can be calculated with (4a)
dxx=45 = (7280 kg/m3) (9.81 m/s2) (45 m)2 / (2 (200×109 N/m2))
= 0.00036 m
= 0.4 mm



