Area Moment of Inertia - Typical Cross Sections II
Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles.
Area Moment of Inertia or Moment of Inertia for an Area - also known as Second Moment of Area - I, is a property of shape that is used to predict deflection, bending and stress in beams.
Area Moment of Inertia for typical Cross Sections II
Angle with Equal Legs
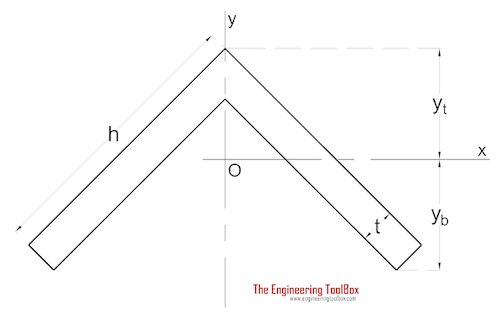
The Area Moment of Inertia for an angle with equal legs can be calculated as
Ix = 1/3 (2 c4 - 2 (c - t)4 + t (h - 2 c + 1/2 t)3) (1a)
where
c = yt cos(45o) (1b)
and
yt = (h2 + ht + t2) / (2 (2 h - t) cos(45o)) (1c)Angle with Unequal Legs

The Area Moment of Inertia for an angle with unequal legs can be calculated as
Ix = 1/3 (t (h - yd)3 + b yd3 - b1 (yd - t)3) (2a)
Iy = 1/3 (t (b - xd)3 + h xd3 - h1 (xd - t)3) (2b)
where
xd = (b2 + h1 t) / (2 (b + h1)) (2c)
yd = (h2 + b1 t) / (2 (h + b1))
Triangle
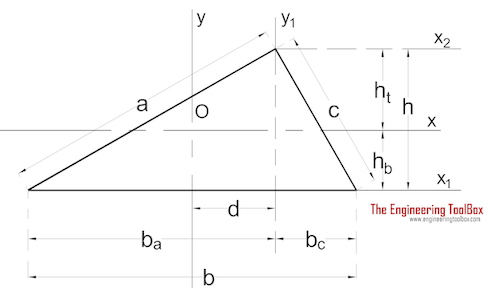
The Area Moment of Inertia for a triangle can be calculated as
Ix = b h3 / 36 (3a)
Iy = h b (b2 - ba bc) / 36 (3b)
Rectangular Triangle
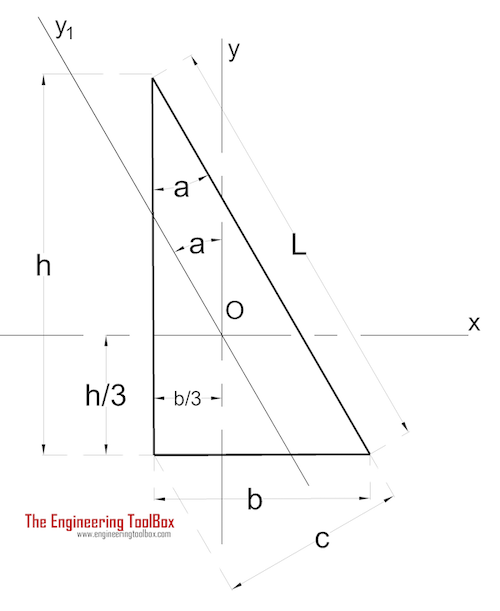
The Area Moment of Inertia for a rectangular triangle can be calculated as
Ix = b h3 / 36 (4a)
Iy =h b3 / 36 (4b)



