Stress, Strain and Young's Modulus
Stress is force per unit area - strain is the deformation of a solid due to stress.
Stress
Stress is the ratio of applied force F to a cross section area - defined as "force per unit area".
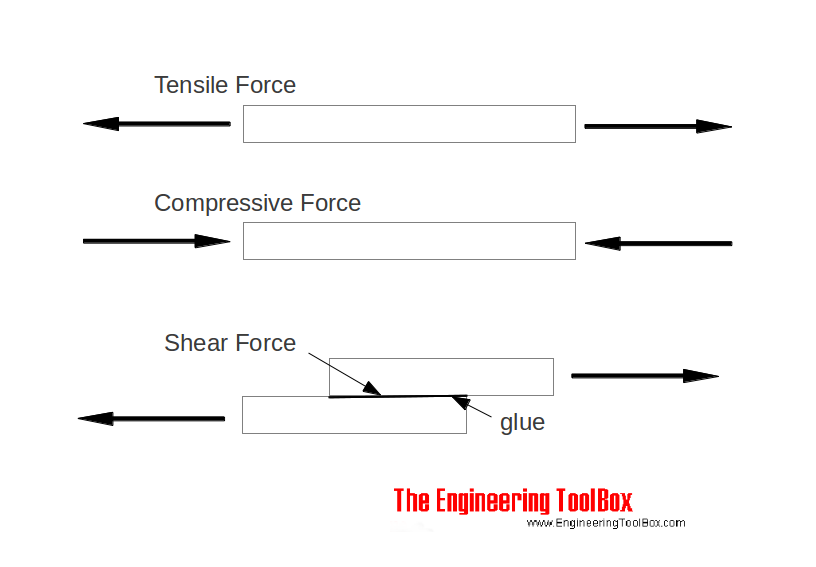
- tensile stress - stress that tends to stretch or lengthen the material - acts normal to the stressed area
- compressive stress - stress that tends to compress or shorten the material - acts normal to the stressed area
- shearing stress - stress that tends to shear the material - acts in plane to the stressed area at right-angles to compressive or tensile stress
Tensile or Compressive Stress - Normal Stress
Tensile or compressive stress normal to the plane is usually denoted "normal stress" or "direct stress" and can be expressed as
σ = Fn / A (1)
where
σ = normal stress (Pa (N/m2), psi (lbf/in2))
Fn = normal force acting perpendicular to the area (N, lbf)
A = area (m2, in2)
- a kip is an imperial unit of force - it equals 1000 lbf (pounds-force)
- 1 kip = 4448.2216 Newtons (N) = 4.4482216 kilo Newtons (kN)
A normal force acts perpendicular to area and is developed whenever external loads tends to push or pull the two segments of a body.
Example - Tensile Force acting on a Rod
A force of 10 kN is acting on a circular rod with diameter 10 mm. The stress in the rod can be calculated as
σ = (10×103 N) / (π ((10×10-3 m) / 2)2)
= 127388535 N/m2
= 127 MPa
Example - Force acting on a Douglas Fir Square Post
A compressive load of 30000 lb is acting on short square 6 x 6 in post of Douglas fir. The dressed size of the post is 5.5 x 5.5 in and the compressive stress can be calculated as
σ = (30000 lb) / ((5.5 in) (5.5 in))
= 991 lb/in2 (psi)
Shear Stress
Stress parallel to a plane is usually denoted as "shear stress" and can be expressed as
τ = Fp / A (2)
where
τ = shear stress (Pa (N/m2), psi (lbf/in2))
Fp = shear force in the plane of the area (N, lbf)
A = area (m2, in2)
A shear force lies in the plane of an area and is developed when external loads tend to cause the two segments of a body to slide over one another.
Strain (Deformation)
Strain is defined as "deformation of a solid due to stress".
- Normal strain - elongation or contraction of a line segment
- Shear strain - change in angle between two line segments originally perpendicular
Normal strain and can be expressed as
ε = dl / lo
= σ / E (3)
where
dl = change of length (m, in)
lo = initial length (m, in)
ε = strain - unit-less
E = Young's modulus (Modulus of Elasticity) (Pa, (N/m2), psi (lbf/in2))
- Young's modulus can be used to predict the elongation or compression of an object when exposed to a force
Note that strain is a dimensionless unit since it is the ratio of two lengths. But it also common practice to state it as the ratio of two length units - like m/m or in/in.
- Poisson's ratio is the ratio of relative contraction strain
Example - Stress and Change of Length
The rod in the example above is 2 m long and made of steel with Modulus of Elasticity 200 GPa (200×109 N/m2). The change of length can be calculated by transforming (3) to
dl = σ lo / E
= (127×106 Pa) (2 m) / (200×109 Pa)
= 0.00127 m
= 1.27 mm
Strain Energy
Stressing an object stores energy in it. For an axial load the energy stored can be expressed as
U = 1/2 Fn dl
where
U = deformation energy (J (N m), ft lb)
Young's Modulus - Modulus of Elasticity (or Tensile Modulus) - Hooke's Law
Most metals deforms proportional to imposed load over a range of loads. Stress is proportional to load and strain is proportional to deformation as expressed with Hooke's Law.
E = stress / strain
= σ / ε
= (Fn / A) / (dl / lo) (4)
where
E = Young's Modulus (N/m2) (lb/in2, psi)
Modulus of Elasticity, or Young's Modulus, is commonly used for metals and metal alloys and expressed in terms 106 lbf/in2, N/m2 or Pa. Tensile modulus is often used for plastics and is expressed in terms 105 lbf/in2 or GPa.
Shear Modulus of Elasticity - or Modulus of Rigidity
G = stress / strain
= τ / γ
= (Fp / A) / (s / d) (5)
where
G = Shear Modulus of Elasticity - or Modulus of Rigidity (N/m2) (lb/in2, psi)
τ = shear stress ((Pa) N/m2, psi)
γ = unit less measure of shear strain
Fp = force parallel to the faces which they act
A = area (m2, in2)
s = displacement of the faces (m, in)
d = distance between the faces displaced (m, in)
Bulk Modulus Elasticity
The Bulk Modulus Elasticity - or Volume Modulus - is a measure of the substance's resistance to uniform compression. Bulk Modulus of Elasticity is the ratio of stress to change in volume of a material subjected to axial loading.
Elastic Moduli
Elastic moduli for some common materials:
| Material | Young's Modulus - E - | Shear Modulus - G - | Bulk Modulus - K - |
|---|---|---|---|
| (GPa) (106 psi) | (GPa) (106 psi) | (GPa) (106 psi) | |
| Aluminum | 70 | 24 | 70 |
| Brass | 91 | 36 | 61 |
| Copper | 110 | 42 | 140 |
| Glass | 55 | 23 | 37 |
| Iron | 91 | 70 | 100 |
| Lead | 16 | 5.6 | 7.7 |
| Steel | 200 | 84 | 160 |
- 1 GPa = 109 Pa (N/m2)
- 106 psi = 1 Mpsi = 103 ksi



