Trigonometric Functions
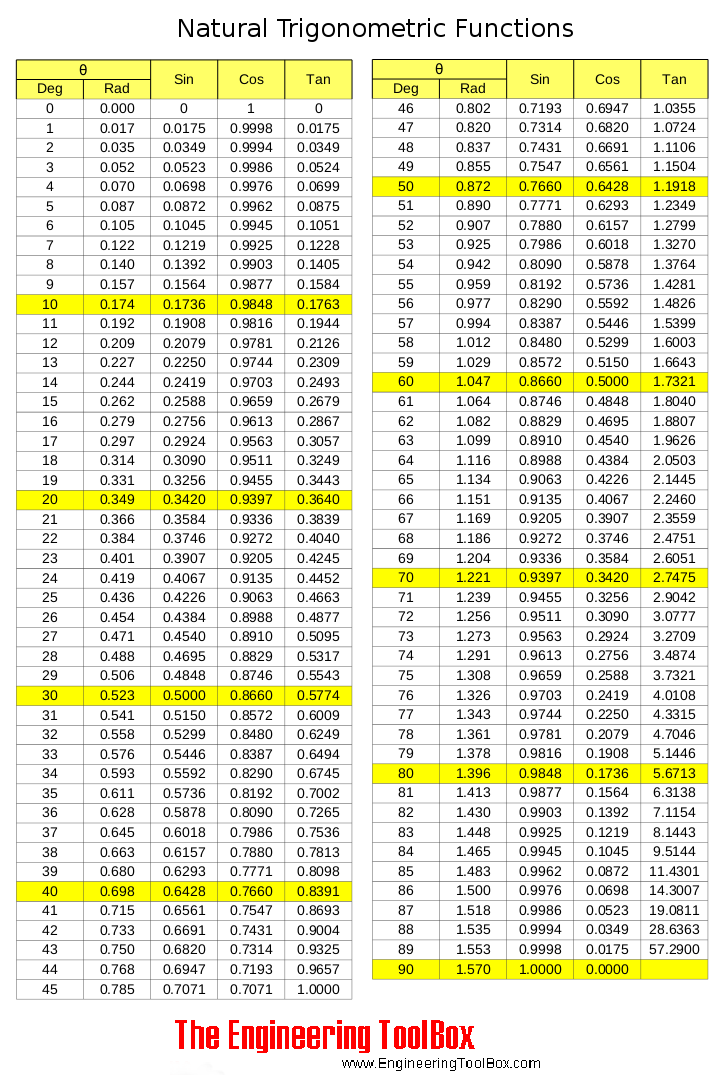
Sine, cosine and tangent - the natural trigonometric functions.
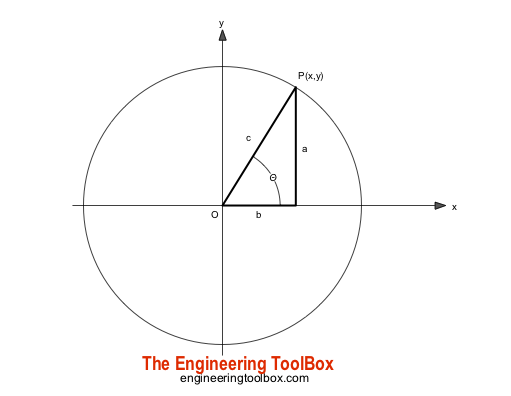
Natural trigonometric functions are expressed as
sin(θd) = a / c
= 1 / csc(θd)
= cos(π/2 - θr) (1)
where
θd = angle in degrees
θr = angle in radians
cos(θd) = b / c
= 1 / sec(θd)
= sin(π/2 - θr) (2)
tan(θd) = a / b
= 1 / cot(θd)
= sin(θd) / cos(θd)
= cot(π/2 - θr ) (3)
cot(θd) = 1 / tan(θd)
= cos(θd) / sin(θd)
= tan(π/2 - θr) (4)
Trigonometric functions ranging 0 to 90 degrees are tabulated below:
Inverse functions
arcsin(a) = sin-1(a) (1a)
arccos(a) = cos-1(a) (2a)
arctan(a) = tan-1(a) (3a)
Addition Formula
sin(a ± b) = sin(a) cos(b) ± cos(a) sin(b) (5)
cos(a ± b) = cos(a) cos(b) ± sin(a) sin(b) (5b)
tan(a ± b) = (tan(a) ± tan(b)) / (1 ± tan(a) tan(b)) (5c)
Sum and Difference Formula
sin(a) + sin(b) = 2 sin((a + b)/2) cos((a + b)/2) (6)
sin(a) - sin(b) = 2 cos((a + b)/2) sin((a - b)/2) (6b)
cos(a) + cos(b) = 2 cos((a + b)/2) cos((a - b)/2) (6c)
cos(a) - cos(b) = - 2 sin((a + b)/2) sin((a - b)/2) (6d)
tan(a) + tan(b) = sin(a + b) / (cos(a) cos(b)) (6e)
tan(a) - tan(b) = sin(a - b) / (cos(a) cos(b)) (6f)
Product Formula
2 sin(a) cos(b) = sin(a - b) + sin(a + b) (7)
2 sin(a) sin(b) = cos(a - b) - cos(a - b) (7b)
2 cos(a) cos(b) = cos(a - b) + cos(a + b) (7c)
Multiple Angle and Powers Formula
sin(2 a) = 2 sin(a) cos(a) (8)
cos(2 a) = cos2(a) - sin2(a) (8b)
cos(2 a) = 2 cos2(a) - 1 (8c)
cos(2 a) = 1 - 2 sin2(a) (8d)
tan(2 a) = 2 tan(a) / (1 - tan2(a)) (8e)
sin2(a) + cos2(a) = 1 (8f)
sec2(a) = tan2(a) + 1 (8g)
Special Triangles
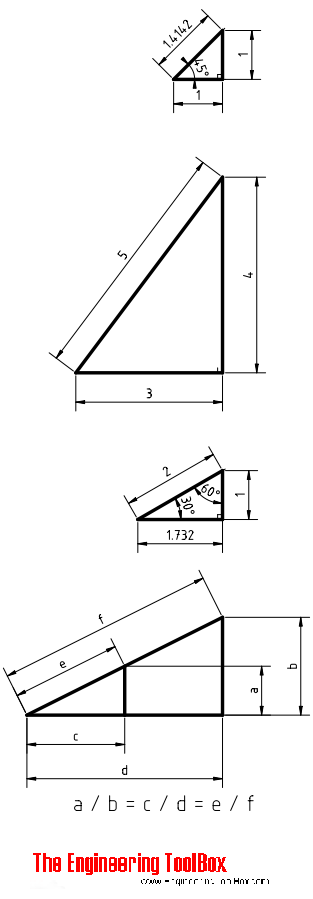
Trigonometric Values
sin(-θd ) = - sin(θd ) (9a)
where
θd = angle in degrees
sin(90° + θd) = cos(θd) (9b)
sin(90° - θd) = cos(θd) (9c)
sin(180° + θd) = - sin(θd) (9d)
sin(180° - θd) = sin(θd) (9e)
sin(270° + θd) = - cos(θd) (9f)
sin(270° - θd) = - cos(θd) (9g)
sin(360° + θd) = sin(θd) (9h)
sin(360° - θd) = - sin(θd) (9h)
cos(-θd) = cos(θd) (10a)
cos(90° + θd) = - sin(θd) (10b)
cos(90° - θd) = sin(θd) (10c)
cos(180° + θd) = - cos(θd) (10d)
cos(180° - θd) = - cos(θd) (10e)
cos(270° + θd) = sin(θd) (10f)
cos(270° - θd) = - sin(θd) (10g)
cos(360° + θd) = cos(θd) (10h)
cos(360° - θd) = cos(θd) (10h)
tan(-θd) = - tan(θd) (11a)
tan(90° + θd) = - cot(θd) (11b)
tan(90° - θd) = cot(θd) (11c)
tan(180° + θd) = tan(θd) (11d)
tan(180° - θd) = - tan(θd) (11e)
tan(270° + θd) = - cot(θd) (11f)
tan(270° - θd) = cot(θd) (11g)
tan(360° + θd) = tan(θd) (11h)
tan(360° - θd) = - tan(θd) (11h)
Trigometric Functions of Common Angles
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| Sin | 0 | 1 / 2 | √2 / 2 | √3 / 2 | 1 |
| Cos | 1 | √2 / 2 | √2 / 2 | 1 / 2 | 0 |
| Tan | 0 | √3 / 3 | 1 | √3 | ∞ |
| Cot | ∞ | √3 | 1 | √3 / 3 | 0 |
| Sec | 1 | 2 √3 / 3 | √2 | 2 | ∞ |
| Cosec | ∞ | 2 | √2 | 2 √3 / 3 | 1 |