Vector Addition
Online vector calculator - add vectors with different magnitude and direction - like forces, velocities and more.
In mechanics there are two kind of quantities
- scalar quantities with magnitude - time, temperature, mass etc.
- vector quantities with magnitude and direction - velocity, force etc.
When adding vector quantities both magnitude and direction are important. Common methods adding coplanar vectors (vectors acting in the same plane) are
- the parallelogram law
- the triangle rule
- trigonometric calculation
The Parallelogram Law
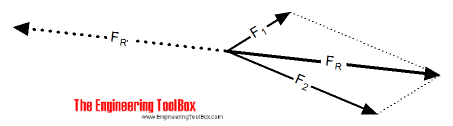
The procedure of "the parallelogram of vectors addition method" is
- draw vector 1 using appropriate scale and in the direction of its action
- from the tail of vector 1 draw vector 2 using the same scale in the direction of its action
- complete the parallelogram by using vector 1 and 2 as sides of the parallelogram
- the resulting vector is represented in both magnitude and direction by the diagonal of the parallelogram
The Triangle Rule
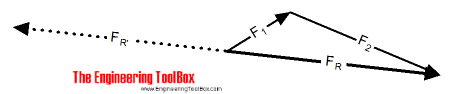
The procedure of "the triangle of vectors addition method" is
- draw vector 1 using appropriate scale and in the direction of its action
- from the nose of the vector draw vector 2 using the same scale and in the direction of its action
- the resulting vector is represented in both magnitude and direction by the vector drawn from the tail of vector 1 to the nose of vector 2
Trigonometric Calculation
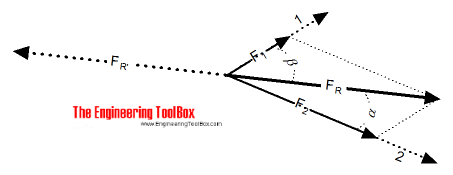
The resulting vector of two coplanar vector can be calculated by trigonometry using "the cosine rule" for a non-right-angled triangle.
FR = (F12 + F22 − 2 F1 F2 cos(180o - (α + β)))1/2 (1)
where
F = the vector quantity - force, velocity etc.
α + β = angle between vector 1 and 2
The angle between the vector and the resulting vector can be calculated using "the sine rule" for a non-right-angled triangle.
α = sin-1(F1 sin(180o - (α + β)) / FR) (2)
where
α + β = the angle between vector 1 and 2 is known
Example - Adding Forces
A force 1 with magnitude 3 kN is acting in direction 80ofrom a force 2 with magnitude 8 kN.
The resulting force can be calculated as
FR = ((3 kN)2 + (8 kN)2 - 2 (5 kN) (8 kN) cos(180o - (80o)))1/2
= 9 (kN)
The angle between vector 1 and the resulting vector can be calculated as
α = sin-1((3 kN) sin(180o - (80o)) / (9 kN))
= 19.1o
The angle between vector 2 and the resulting vector can be calculated as
α = sin-1( (8 kN) sin(180o - (80o)) / (9 kN))
= 60.9o
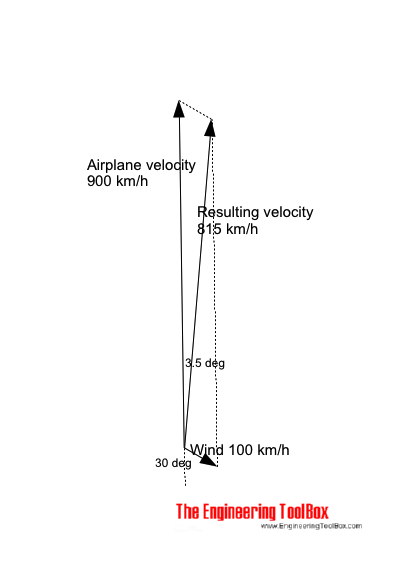
Example - Airplane in Wind
A headwind of 100 km/h is acting 30o starboard on an airplane with velocity 900 km/h.
The resulting velocity for the airplane related to the ground can be calculated as
vR = ((900 km/h)2 + (100 km/h)2 - 2 (900 km/h) (100 km/h) cos(180o - (30o)))1/2
= 815 (km/h)
The angle between the airplane course and actual relative ground course can be calculated as
α = sin-1((100 km/h) sin((180o) - (30o)) / (815 km/h))
= 3.5o
Vector Calculator
The generic calculator below is based on equation (1) and can be used to add vectors quantities like velocities, forces etc.
Parallelogram
Resultant vectors can be estimated by drawing parallelograms as indicated below.
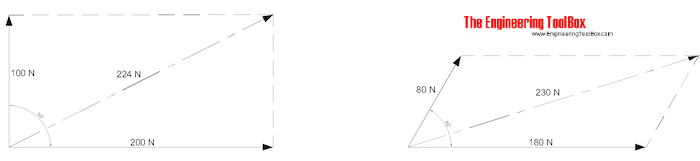
- draw the vectors with right direction and magnitude
- draw parallel lines to the vectors
- draw the resultant vector to the crossing point between the parallel lines
- measure the magnitude and direction of the resultant vector in the drawing
The method can also be used with more than two vectors as indicated below.
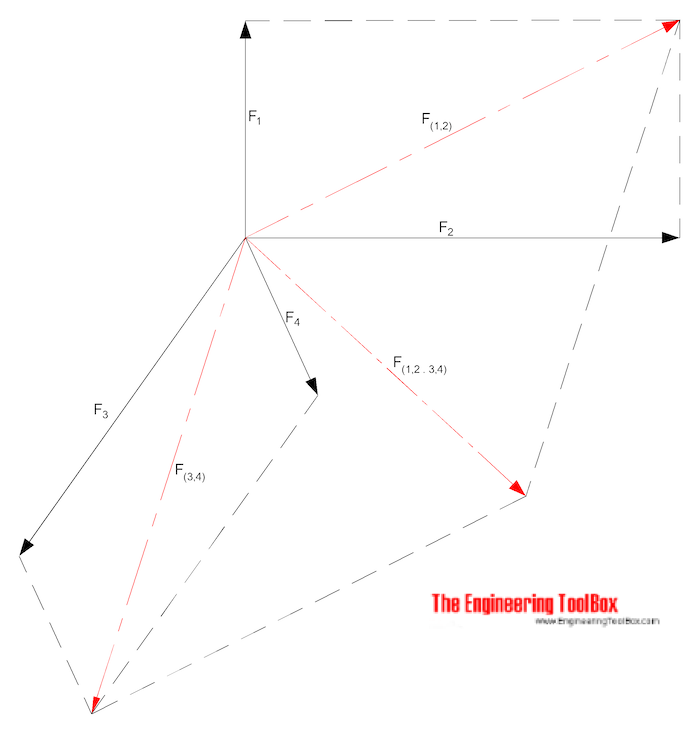
- draw the resultant vectors between two and two vectors
- draw the resultant vectors between two and two of resultant vectors
- continue until there is only one final resultant vector
- measure direction and magnitude of the final resultant vector in the drawing
In the example above - first find the resultant F(1,2) by adding F1 and F2, and the resultant F(3,4) by adding F3 and F4. The find the resultant F(1,2.3,4) by adding F(1,2) and F(3,4).