Impact Force
Impact forces acting on falling objects hitting the ground, cars crashing and similar cases.

The dynamic kinetic energy of a moving object, like a falling ball or a driving car, can be expressed as
E = 1/2 m v2 (1)
where
E = kinetic (dynamic) energy (J, ft lb)
m = mass of the object (kg, slugs )
v = velocity of the object (m/s, ft/s)
In an impact - like a car crash - the work made by the impact force slowing down an moving object over a distance by deforming the crumple zone can be expressed as
W = Favg s (2)
where
W = work done (J, ft lb)
Favg = average impact force during deformation (N, lbf)
s = deformation distance, crumple zone (m, ft)
When a crumple zone deforms in a car crash the average impact force is designed to be as constant as possible.
In an impact where the object is not deformed - the work made by the impact force slowing down the moving object equals to the work done by a spring force - and can be expressed as
W = 1/2 Fmax s
= 1/2 k s2 (2b)
where
W = work done (J, ft lb)
Fmax = maximum force at the end of the deformation (N, lbf)
k = spring constant
s = deformation distance (m, ft)
In a car crash the dynamic energy is converted to work and equation 1 and 2 can be combined to
Favg s = 1/2 m v2 (3)
The average impact force can be calculated as
Favg = 1/2 m v2 / s (3b)
The deformation slow-down distance can be calculated as
s = 1/2 m v2 / Favg (3c)
Note! - The deformation slow-down distance is very important and the key to limit the forces acting on passengers in a car crash.
Example - Car Crash
A car with a mass of 2000 kg drives with speed 60 km/h (16.7 m/s) before it crashes into a massive concrete wall. The front of the car impacts 0.5 m (the deformation distance).
The impact force can be calculated as
Fmax = 1/2 (2000 kg) (16.7 m/s)2 / (0.5 m)
= 558 kN
Note that the gravitation force (weight) acting on the car is only
Fw = m g
= (2000 kg) (9.81 m/s2)
= 19.6 kN
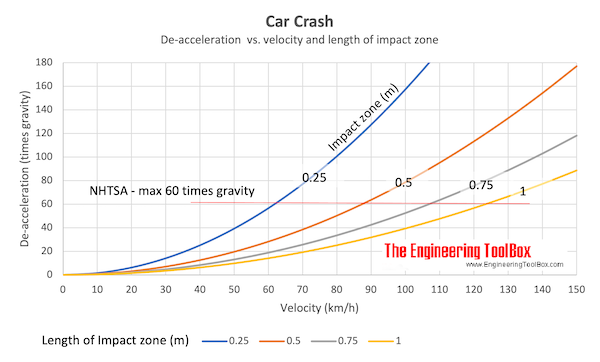
The impact creates a force 28 times gravity!!
A person sitting inside the car with seat belts on will de-accelerate with a force 28 times gravity . Note that the National Highway Traffic Safety Administration (NHTSA) states that "the maximum chest acceleration shall not exceed 60 times gravity for time periods longer than 3 milliseconds ". For a car crash with 90 km/h (25 m/s) the de-acceleration will be 64 times gravity (same parameters as above).
- 60 mph = 96.6 km/h
Impact Force from a Falling Object
The dynamic energy in a falling object at the impact moment when it hits the ground can be calculated as
E = Fweight h
= m ag h (4)
where
Fweight = force due to gravity - or weight (N, lbf)
ag = acceleration of gravity (9.81 m/s2, 32.17405 ft/s2)
h = falling height (m)
If the dynamic energy from the fall is converted to impact work - equation 2 and 4 can be combined to
Favg s = m ag h (5)
The impact force can be expressed as
Favg = m ag h / s (5b)
The deformation slow-down distance can be expressed as
s = m ag h / Favg (5c)
Example - a Falling Car
The same car as above falls from height 14.2 m and crashes on the crumple zone with the front down on a massive concrete tarmac. The front impacts 0.5 m (slow down distance) as above. The impact force can be calculated as
Favg = (2000 kg) (9.81 m/s2) (14.2 m) / (0.5 m)
= 558 kN
Note! - a car crash in 90 km/h (25 m/s) compares to a fall from 32 m !!
Example - a Person falling from a Table
A person with weight (gravitational force) of 200 lbs (lbf) falls from a 4 feet high table.
The energy of the falling body when it hits the ground can be calculated using (4) as
E = (200 lbf) (4 ft)
= 800 ft lb
The impact on a human body can be difficult to determine since it depends on how the body hits the ground - which part of the body, the angle of the body and/or if hands are used to protect the body and so on.
For this example we use an impact distance of 3/4 inch (0.0625 ft) to calculate the impact force:
Favg = (800 ft lb) / (0.0625 ft)
= 12800 lbf
In metric units - person with weight 90 kg, falling distance 1.2 m and impact distance 2 cm :
E = (90 kg) (9.81 m/s2) (1.2 m)
= 1059 J
Favg = (1059 J) / (0.02 m)
= 53 kN



