Manning's Formula and Gravity Flow
Calculate cross-sectional average velocity flow in open channels.
Manning's equation is an empirical equation that can be used to calculate cross-sectional average velocity flow in open channels
v = (kn / n) Rh 2/3 S1/2 (1)
where
v = cross-sectional mean velocity (ft/s, m/s)
kn = 1.486 for English units and kn = 1.0 for SI units
n = Manning coefficient of roughness - ranging from 0.01 (a clean and smooth channel) to 0.06 (a channel with stones and debris, 1/3 of vegetation)
Rh = hydraulic radius (ft, m)
S = slope - or gradient - of pipe (ft/ft, m/m)
The Manning coefficients n in the English (Imperial) are equal to the coefficients in the SI system. The Manning coefficient is not dimensionless but the units are often omitted.
Units for (kn / n) in the SI system vs. the Imperial system can be expressed as:
(kn / n) = m1/3 / s
= 1.4859 ft1/3 / s
Hydraulic radius can be expressed as
Rh = A / Pw (2)
where
A = cross sectional area of flow (ft2, m)
Pw = wetted perimeter (ft, m)
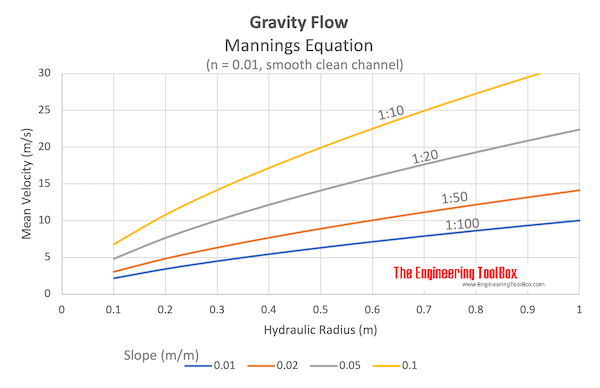
Download and print Gravity Flow - Mannings Equation Chart
The volume flow in the channel can be calculated as
q = A v
= A (kn / n) Rh 2/3 S1/2 (3)
where
q = volume flow (ft3/s, m3/s)
A = cross-sectional area of flow (ft2, m2)
Example - Flow in an Open Channel
A channel with the shape of an half circle is 100% filled. The diameter of the half circle is 500 mm (0.5 m) and the channel is made of concrete with Manning coefficient 0.012 . The slope of the channel is 1/100 m/m .

make 3D models with the free Engineering ToolBox Sketchup Extension !
The cross section area of the half circle flow can be calculated as
A = (0.5 π ((0.5 m) / 2)2)
= 0.098 m2
The wetted perimeter of the half circle flow can be calculated as
P = 0.5 2 π (0.5 m) / 2)
= 0.785 m
The hydraulic radius of the channel can be calculated from (2) as
Rh = A / P
= ( 0.098 m2>) / ( 0.785 m)
= 0.125 m
The cross sectional mean velocity can be calculated from (1) as
v = (kn / n) Rh 2/3 S1/2
= (1.0 / 0.012) (0.125 m)2/3 (1/100 m/m)1/2
= 2.1 m/s
The volume flow can be calculated from (3) as
q = A v
= ( 0.098 m2) (2.1 m/s)
= 0.20 m3/s
Gravity Flow Calculator - Half Filled Circular Pipe
The Gravity Flow Calculator is based on the equations and the example above above. It's valid for half filled circular pipe.



