Torsion of Shafts

The torsion of solid or hollow shafts - Polar Moment of Inertia of Area.

Shear Stress in the Shaft

When a shaft is subjected to a torque or twisting a shearing stress is produced in the shaft. The shear stress varies from zero in the axis to a maximum at the outside surface of the shaft.

The shear stress in a solid circular shaft in a given position can be expressed as:

τ = T r / J (1)

where

τ = shear stress (Pa, lb_f/ft² (psf))

T = twisting moment (Nm, lb_f ft)

r = distance from center to stressed surface in the given position (m, ft)

J = Polar Moment of Inertia of Area (m⁴, ft⁴)

Note

the "Polar Moment of Inertia of an Area" is a measure of a shaft's ability to resist torsion. The "Polar Moment of Inertia" is defined with respect to an axis perpendicular to the area considered. It is analogous to the "Area Moment of Inertia" - which characterizes a beam's ability to resist bending - required to predict deflection and stress in a beam.
1 ft = 12 in
1 ft⁴ = 20736 in⁴
1 psf (lb_f/ft²) = 1/144 psi (lb_f/in²)

"Polar Moment of Inertia of an Area" is also called "Polar Moment of Inertia", "Second Moment of Area", "Area Moment of Inertia", "Polar Moment of Area" or "Second Area Moment".

Polar Moment of Inertia vs. Area Moment of Inertia

"Polar Moment of Inertia" - a measure of a beam's ability to resist torsion - which is required to calculate the twist of a beam subjected to torque
"Area Moment of Inertia" - a property of shape that is used to predict deflection, bending and stress in beams

Circular Shaft and Maximum Moment or Torque

Maximum moment in a circular shaft can be expressed as:

T_max = τ_max J / R (2)

where

T_max = maximum twisting torque (Nm, lb_f ft)

τ_max = maximum shear stress (Pa, lb_f/ft²)

R = radius of shaft (m, ft)

Combining (2) and (3) for a solid shaft

T_max = (π / 16) τ_max D³ (2b)

Combining (2) and (3b) for a hollow shaft

T_max = (π / 16) τ_max (D⁴ - d⁴) / D (2c)

Circular Shaft and Polar Moment of Inertia

Polar Moment of Inertia of a circular solid shaft can be expressed as

J = π R⁴ / 2

= π (D / 2)⁴ / 2

= π D⁴ / 32 (3)

where

D = shaft outside diameter (m, in)

Polar Moment of Inertia of a circular hollow shaft can be expressed as

J = π (D⁴ - d⁴) / 32 (3b)

where

d = shaft inside diameter (m, ft)

Diameter of a Solid Shaft

Diameter of a solid shaft can calculated by the formula

D = 1.72 (T_max / τ_max)^1/3 (4)

Torsional Deflection of Shaft

Torsion deflection of shaft

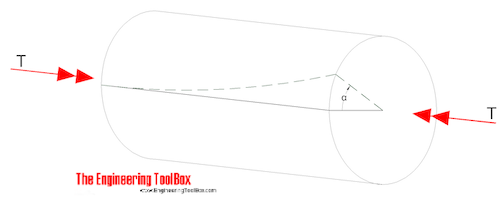
The angular deflection of a torsion shaft can be expressed as

α = L T / (JG) (5)

where

α = angular shaft deflection (radians)

L = length of shaft (m, ft)

G = Shear Modulus of Rigidity - or Modulus of Rigidity (Pa, psf)

The angular deflection of a torsion solid shaft can be expressed as

α = 32 L T / (G π D⁴) (5a)

The angular deflection of a torsion hollow shaft can be expressed as

α = 32 L T / (G π (D⁴- d⁴)) (5b)

The angle in degrees can be achieved by multiplying the angle θ in radians with 180 / π.

Solid shaft (π replaced)

α_degrees ≈ 584 L T / (G D⁴) (6a)

Hollow shaft (π replaced)

α_degrees ≈ 584 L T / (G (D⁴- d⁴) (6b)

Torsion Resisting Moments from Shafts of Various Cross Sections

	Maximum Torsional Resisting Moment - T_max - (Nm, lb_f ft)	Nomenclature
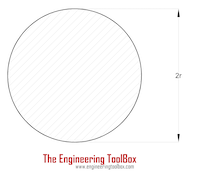Solid Cylinder Shaft	(π / 16) τ_max (2 r)³ = (π / 16) τ_max D³
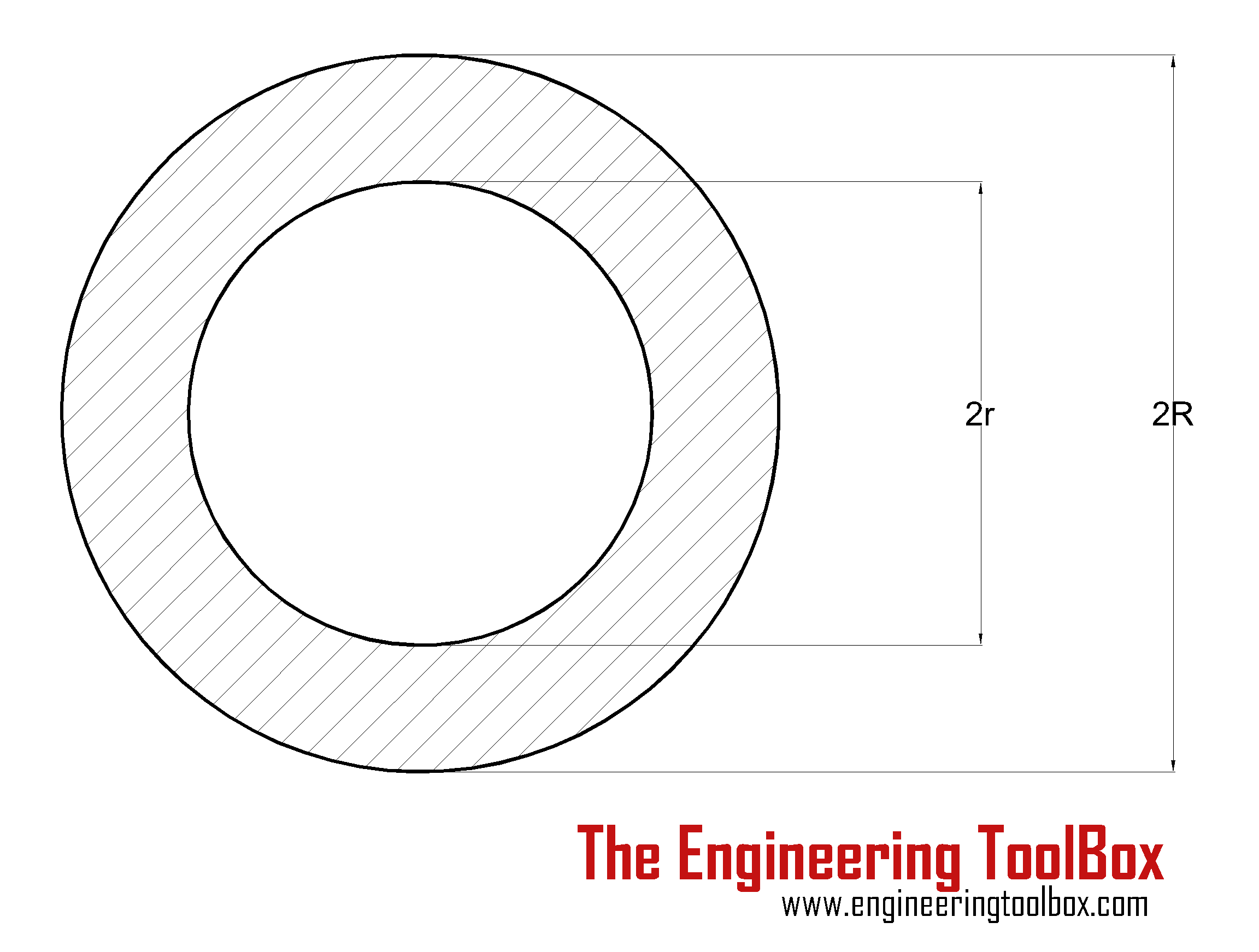Hollow Cylinder Shaft	(π / 16) τ_max ((2 R)⁴ - (2 r)⁴) / (2 R) = (π / 16) τ_max (D⁴ - d⁴) / D
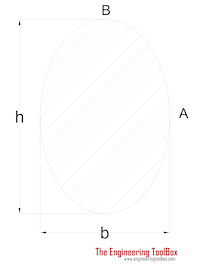Ellipse Shaft	(π / 16) τ_max b² h	h = "height" of shaft b = "width" of shaft h > b
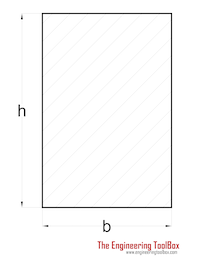Rectangle Shaft	(2 / 9) τ_max b² h	h > b
Square Shaft	(2 / 9) τ_max H³
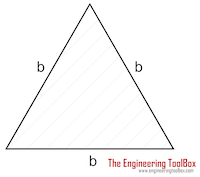Triangle Shaft	(1 / 20) τ_max b³	b = length of triangle side
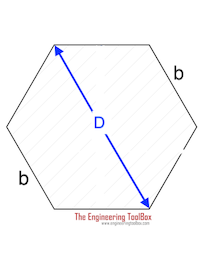Hexagon Shaft	0.123τ_maxD³ 0.189 τ_{max b}³

Example - Shear Stress and Angular Deflection in a Solid Cylinder

A moment of 1000 Nm is acting on a solid cylinder shaft with diameter 50 mm (0.05 m) and length 1 m. The shaft is made in steel with modulus of rigidity 79 GPa (79 10⁹ Pa).

Maximum shear stress can be calculated as

τ_max = T r / J

= T (D / 2) / (π D⁴ / 32)

= (1000 Nm) ((0.05 m) / 2) / (π (0.05 m)⁴ / 32)

= 40764331 Pa

= 40.8 MPa

The angular deflection of the shaft can be calculated as

θ = L T / (J G)

= L T / ((π D⁴ / 32) G)

= (1 m) (1000 Nm) / ((π (0.05 m)⁴ / 32) (79 10⁹ Pa))

= 0.021 (radians)

= 1.2^o

Example - Shear Stress and Angular Deflection in a Hollow Cylinder

A moment of 1000 Nm is acting on a hollow cylinder shaft with outer diameter 50 mm (0.05 m), inner diameter 30 mm (0.03 m) and length 1 m. The shaft is made in steel with modulus of rigidity 79 GPa (79 10⁹ Pa).

Maximum shear stress can be calculated as

τ_max = T r / J

= T (D / 2) / (π (D⁴ - d⁴) / 32)

= (1000 Nm) ((0.05 m) / 2) / (π ((0.05 m)⁴ - (0.03 m)⁴) / 32)

= 46.8 MPa

The angular deflection of the shaft can be calculated as

θ = L T / (J G)

= L T / ((π D⁴ / 32) G)

= (1 m) (1000 Nm) / ((π ((0.05 m)⁴ - (0.03 m)⁴) / 32) (79 10⁹ Pa))

= 0.023 radian)

= 1.4^o

Example - Required Shaft Diameter to Transmit Power

Electric motor

A 15 kW electric motor shall be used to transmit power through a connected solid shaft. The motor and the shaft rotates with 2000 rpm. The maximum allowable shear stress - τ_max - in the shaft is 100 MPa.

The connection between power and torque can be expressed

P = 0.105 n_rpm T (7)

where

P = power (W)

n_rpm = speed of shaft (rpm)

Re-arranged and with values - the torque can be calculated

T = (15 10³ W) / (0.105 (2000 rpm))

= 71 Nm

Minimum diameter of the shaft can be calculated with eq. 4

D = 1.72 ((71 Nm) / (100 10⁶ Pa))^1/3

= 0.0153 m

= 15.3 mm