Static Pressure vs. Head
Static pressure vs. pressure head in fluids.
Pressure indicates the normal force per unit area at a given point acting on a given plane. Since there is no shearing stresses present in a fluid at rest - the pressure in a fluid is independent of direction.
For fluids - liquids or gases - at rest the pressure gradient in the vertical direction depends only on the specific weight of the fluid.
How pressure changes with elevation in a fluid can be expressed as
Δp = - γ Δh (1)
where
Δp = change in pressure (Pa, psi)
Δh = change in height (m, in)
γ = specific weight of fluid (N/m3, lb/ft3)
The pressure gradient in vertical direction is negative - the pressure decrease upwards.
Specific Weight
Specific Weight of a fluid can be expressed as:
γ = ρ g (2)
where
ρ = density of fluid (kg/m3, slugs /ft3)
g = acceleration of gravity (9.81 m/s2, 32.174 ft/s2)
In general the specific weight - γ - is constant for fluids. For gases the specific weight - γ - varies with elevation (and compression).
The pressure exerted by a static fluid depends only upon
- the depth of the fluid
- the density of the fluid
- the acceleration of gravity
Static Pressure in a Fluid
For a incompressible fluid - as a liquid - the pressure difference between two elevations can be expressed as:
Δp = p2 - p1
= - γ (h2 - h1) (3)
where
p2 = pressure at level 2 (Pa, psi)
p1 = pressure at level 1 (Pa, psi)
h2 = level 2 (m, ft)
h1 = level 1 (m, ft)
(3) can be transformed to:
Δp = p1 - p2
= γ (h2 - h1) (4)
or
p1 - p2 = γ Δh (5)
where
Δh = h2 - h1 = difference in elevation - the dept down from location h2 to h1 (m, ft)
or
p1 = γ Δh + p2 (6)
Example - Pressure in a Fluid
The absolute pressure at water depth of 10 m can be calculated as:
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 or Pa) + (101300 Pa)
= 199400 Pa
= 199.4 kPa
where
ρ = 1000 kg/m3
g = 9.81 m/s2
p2= pressure at surface level = atmospheric pressure = 101.3 kPa
The gauge pressure can be calculated by setting p2= 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98.1 kPa
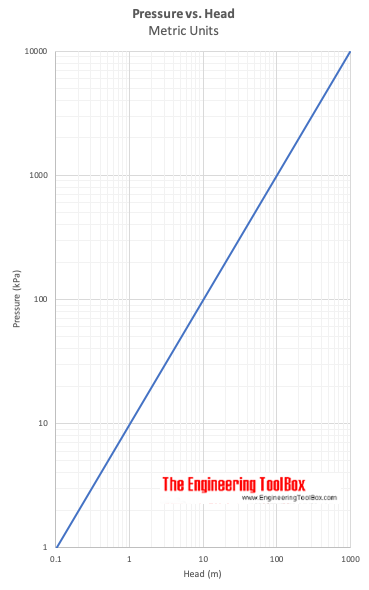
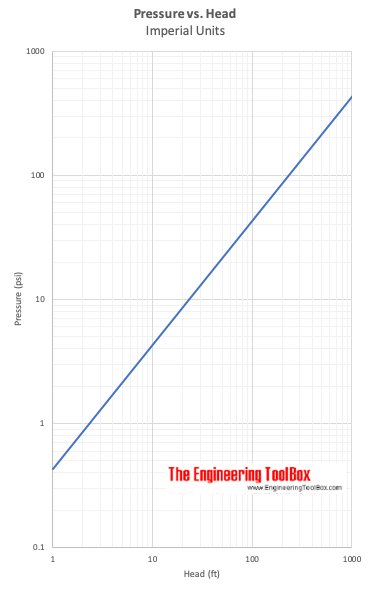
Pressure vs. Head
(6) can be transformed to:
Δh = (p2 - p1) / γ (7)
Δh express head - the height difference of a column of fluid of specific weight - γ - required to give a pressure difference Δp = p2 - p1 .
Example - Pressure vs. Head
A pressure difference of 5 psi (lbf/in2) is equivalent to head in water
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11.6 ft of water
or head in Mercury
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0.85 ft of mercury
Specific weight of water is 62.4 (lb/ft3) and specific weight of mercury is 847 (lb/ft3) .