Sound Power
Sound power from sources like fans, jet engines, cars, humans and more.
Sound Power (W)
Sound power is the energy rate, or energy of sound per unit of time (J/s or W in SI-units) - emitted by a source.
When sound propagates through a medium acoustic sound power is transferred. The sound intensity is the sound power transmission through a surface (W/m2) - a vector quantity with direction through a surface. The sound power radiated from a source can therefore be calculated by integrating the acoustic intensity over a surrounding surface.
N = ∫S I·n dS (1)
where
N = acoustic power radiated from source (W)
I = sound intensity - sound power through surface (W/m2)
n = unit vector normal to surface area
S = surface area surrounding source (m2)
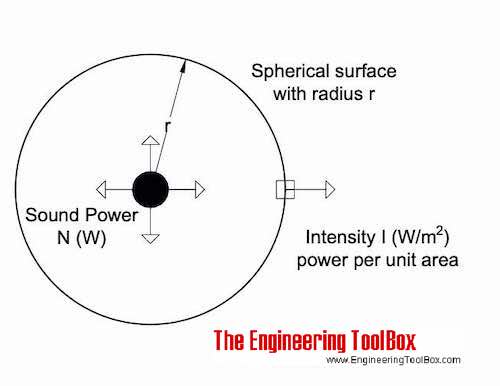
For a source propagating sound in all directions - through a virtual spherical surface - the acoustic power can be modified to
N = 4 π r2 I (1b)
where
r = radius in sphere (m)
Sound Power Level (dB)
It can be practical to express the sound power relative a reference power - 10-12 W - in a logarithmic "decibel" scale as
LN = 10 log10(N / Nref)
= 10 log10(N) + 120 (2)
where
LN = sound power level (decibel, dB)
N = sound power (W)
Nref = 10-12 - reference sound power (W)
The human ear is able hear sound powers that spans from 10-12 W to 10 - 100 W, a range of 10/10-12 = 1013.
Example - Sound Power Level
The sound power from a from a tool is 0.0015 W. The sound power level can be calculated as
LN = 10 log10 ((0.0015 W) / (10-12 W))
= 91.8 dB
The sound power level from a machine is rated to 100 dB. The sound power can be calculated by rearranging (1) to
N = 10((LN - 120) / 10)
= 10(((100 dB) - 120) / 10)
= 0.01 W
Sound Intensity Level (dB)
Sound intensity can also be expressed relative to a reference intensity - the threshold of hearing - 10-12 W/m2 - in a logarithmic "decibel" scale as
LI = 10 log10(I / Iref)
= 10 log10(I) + 120 (3)
where
LI = sound intensity level (decibel, dB)
I = sound intensity (W/m2)
Iref = 10-12 - reference sound intensity (W/m2)
The value of sound intensity level and sound pressure level is almost the same
LI = Lp - 0.2 (4)
where
Lp = sound pressure level (dB)
Example - Sound Intensity and Pressure Level - Distance from Source
The sound intensity - sound power transfer per unit surrounding surface - in a distance 1 m from the 100 dB machine in the example above can be calculated by rearranging (1b) to
I = N / (4 π r2)
= (0.01 W) / (4 π (1 m)2)
= 0.0008 W/m2
The sound intensity level can be calculated with (3) as
LI ≈ Lp ≈ 10 log10(0.0008 W/m2) + 120
= 89 dB
The sound intensity in distance 10 m
I = N / (4 π r2)
= (0.01 W) / (4 π (10 m)2)>
= 0.000008 W/m2
The sound intensity level can be calculated with (3) as
LI ≈ Lp ≈ 10 log10(0.000008 W/m2) + 120
= 69 dB
Typical Sound Power
Sound power in watts and sound power level in decibels from some common sources are indicated below:
| Source | Sound Power - N - (W) | Sound Power Level - N - (dB) (ref 10-12 W) |
|---|---|---|
| Saturn Rocket | 100,000,000 | 200 |
| Turbo Jet Plane Engine | 100,000 | 170 |
| 10,000 | 160 | |
| Inside jet engine test cell Jet Plane Take-off |
1,000 | 150 |
| Large centrifugal fan, 800.000 m3/h Turbo Propeller Plane at take-off |
100 | 140 |
| Axial fan, 100.000 m3/h Machine Gun Large Pipe Organ |
10 | 130 |
| Large chipping hammer Symphonic orchestra Jet Plane from passenger ramp Heavy Thunder Sonic Boom Small aircraft engine Tractor 150 hp |
1 | 120 |
| Centrifugal fan, 25.000 m3/h Accelerating Motorcycle Heavy Metal, Hard Rock Band Music Blaring radio Chain Saw Wood Working Shop Large air Compressor Electric motor 100 hp/2600 rpm |
0.1 | 110 |
| Air chisel Subway Steel Wheels Magnetic drill press High pressure gas leak Banging of steel plate Drive gear Car at Highway Speed Normal Fan Vacuum Pump Banging Steel Plate Wood Planer Air Compressor Propeller Plane Outboard motor Loud street noise Power Lawn Mover Pneumatic drill Helicopter |
0.01 | 100 |
| Cut-off saw Hammer mill Small air compressor Grinder Heavy diesel vehicle Heavy city traffic Lawn mover Airplane Cabin at normal flight Kitchen Blender Spinning Machines Subway train Pneumatic Jackhammer |
0.001 | 90 |
| Alarm clock Vacuum Cleaner Dishwasher |
0.0001 | 80 |
| Toilet Flushing Printing Press Inside Railroad Car Noisy Office Inside Automobile Clothes Dryer |
0.00001 | 70 |
| Large department store Busy restaurant or canteen Ventilation Fan Noisy Home Average Office Hair Dryer |
0.000001 | 60 |
| Room with window air conditioner Office Air Diffuser Quiet Office Average Home Quit Street |
0.0000001 | 50 |
| Voice, low Small Electric Clock Private Office Quiet Home Refrigerator Bird Singing Ambient Wilderness Agricultural Land |
0.00000001 | 40 |
| Room in a quiet dwelling at midnight Quiet Conversation Background noise in broadcast/recording studio |
0.000000001 | 30 |
| Rustling leaves Empty Auditorium Whisper Watch Ticking Rural Ambient |
0.0000000001 | 20 |
| Human Breath | 0.00000000001 | 10 |
| 0.000000000001 | 0 |
Related Topics
-
Acoustics
Room acoustics and acoustic properties. decibel A, B and C calculations. Noise Rating (NR) curves. Sound transmission through walls. Calculate sound pressure, sound intensity and sound attenuation. -
Noise and Attenuation
Noise is usually defined as unwanted sound - noise, noise generation, silencers and attenuation in HVAC systems.
Related Documents
-
Fans - Noise Power Generation
The sound generated by a fan depends on the motor power, the volume capacity, the static pressure increase and the discharged volume. -
Maximum Sound Pressure Levels in Rooms
Maximum recommended sound pressure levels in rooms like kindergartens, auditoriums, libraries, cinemas and more. -
Noise - Acceptable dBA Level
Acceptable noise - dBA - level at typical common locations. -
Noise generated by Fans - Blade Pass Frequency (BPF)
TheBlade Pass Frequency noise generated by a fan can be very intense and varies with the number of blades and the rotation velocity. -
Noise generated in Blade Dampers
Sound power noise generated by blade dampers in ventilation systems. -
Outdoor Ambient Sound Pressure Levels
Outdoor ambient sound pressure levels (dBA) in rural and urban business and industrial environments with or without limited traffic. -
Phonetic Alphabet
The phonetic alphabet used in international aircraft communications. -
Signals - Adding Decibels
The logarithmic decibel scale is convenient when adding signal values like sound power, pressure and others from two or more sources. -
SIL - the Speech Interference Levels
Background noise frequencies that interferes with speech. -
Sound - Abatement vs. the Distance from Source
The disruption of the sound pressure wave and the reduction of noise is called attenuation - Sound Pressure Level vs. distance calculator. -
Sound - Attenuation and the Directivity Coefficient
The attenuation in a room depends on the location of the sound source and the receiver - and the room constant. -
Sound - Doppler Effect
The doppler effect is the change in sound frequency due to the relative motion between a source and a listener. -
Sound Intensity
Acoustic power of sound per unit area. -
Sound Intensity, Power and Pressure Levels
Introduction to decibel, sound power, intensity and pressure. -
Use of Telephones in Noisy Areas
Satisfactory, difficult and impossible noise levels for telephone use in noisy areas.
