Bulk Modulus and Fluid Elasticities
Introduction to - and definition of - Bulk Modulus Elasticity commonly used to characterize the compressibility of fluids.
The Bulk Modulus Elasticity - or Volume Modulus - is a material property characterizing the compressibility of a fluid - how easy a unit volume of a fluid can be changed when changing the pressure working upon it. It is the ratio of the
change in unit pressure to the corresponding volume change per unit of volume.
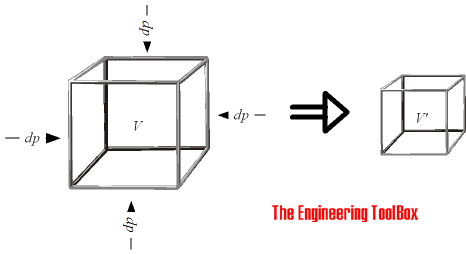
The Bulk Modulus Elasticity can be calculated as
K = - dp / (dV / V0)
= - ( p1 - p0) / ((V1 - V0) / V0) (1)
where
K = Bulk Modulus of Elasticity (Pa, N/m2)
dp = differential change in pressure on the object (Pa, N/m2)
dV = differential change in volume of the object (m3)
V0 = initial volume of the object (m3)
p0 = initial pressure ( Pa, N/m2)
p1 = final pressure ( Pa, N/m2)
V1 = final volume ( m3)
The Bulk Modulus Elasticity can alternatively be expressed as
K = dp / (dρ / ρ0)
= (p1 - p0) / ((ρ1 - ρ0) / ρ0) (2)
where
dρ = differential change in density of the object (kg/m3)
ρ0 = initial density of the object (kg/m3)
ρ1 = final density of the object ( kg/m3)
An increase in the pressure will decrease the volume (1). A decrease in the volume will increase the density (2) .
- The SI unit of the bulk modulus elasticity is N/m2 (Pa)
- The imperial (BG) unit is lbf/in2 (psi)
- 1 lbf/in2(psi) = 6.894×103 N/m2 (Pa)
A large Bulk Modulus indicates a relative incompressible fluid.
Bulk Modulus Common Fluids
| Fluid | Bulk Modulus - K - | |
|---|---|---|
| Imperial Units - BG ( 105 psi, lbf/in2) | SI Units ( 109 Pa, N/m2) | |
| Acetone | 1.34 | 0.92 |
| Benzene | 1.5 | 1.05 |
| Carbon Tetrachloride | 1.91 | 1.32 |
| Ethyl Alcohol | 1.54 | 1.06 |
| Gasoline | 1.9 | 1.3 |
| Glycerin | 6.31 | 4.35 |
| ISO 32 mineral oil | 2.6 | 1.8 |
| Kerosene | 1.9 | 1.3 |
| Mercury | 41.4 | 28.5 |
| Paraffin Oil | 2.41 | 1.66 |
| Petrol | 1.55 - 2.16 | 1.07 - 1.49 |
| Phosphate ester | 4.4 | 3 |
| SAE 30 Oil | 2.2 | 1.5 |
| Seawater | 3.39 | 2.34 |
| Sulfuric Acid | 4.3 | 3.0 |
| Water (10 oC) | 3.12 | 2.09 |
| Water - glycol | 5 | 3.4 |
| Water in oil emulsion | 3.3 | 2.3 |
- 1 GPa = 109 Pa (N/m2)
Stainless steel with Bulk Modulus 163×109 Pa is aprox. 80 times harder to compress than water with Bulk Modulus 2.15×109 Pa .
Example - Density of Seawater in the Mariana Trench
- the deepest known point in the Earth's oceans - 10994 m .
The hydrostatic pressure in the Mariana Trench can be calculated as
p1 = (1022 kg/m3) (9.81 m/s2) (10994 m)
= 110 106 Pa (110 MPa)
The initial pressure at sea-level is 105 Pa and the density of seawater at sea level is 1022 kg/m3 .
The density of seawater in the deep can be calculated by modifying (2) to
ρ1 = ((p1 - p0) ρ0 + K ρ0) / K
= (((110×106 Pa) - (1×105 Pa)) (1022 kg/m3) + (2.34×109 Pa) (1022 kg/m3)) / ( 2.34×109 Pa)
= 1070 kg/m3
Note! - since the density of the seawater varies with dept the pressure calculation could be done more accurate by calculating in dept intervals.
Bulk Modulus of Water vs. Temperature
| Temperature (oC) | Bulk Modulus (109 Pa) |
|---|---|
| 0.01 | 1.96 |
| 10 | 2.09 |
| 20 | 2.18 |
| 30 | 2.23 |
| 40 | 2.26 |
| 50 | 2.26 |
| 60 | 2.25 |
| 70 | 2.21 |
| 80 | 2.17 |
| 90 | 2.11 |
| 100 | 2.04 |



