Earth Pressure Acting on Basement Walls
Calculate lateral earth pressure acting on basement walls.
1st Floor above Ground Level
The forces that keeps the basement wall in position - the force at the basement floor/slab and the force from the 1st floor joists above ground level - are indicated in the figure below.
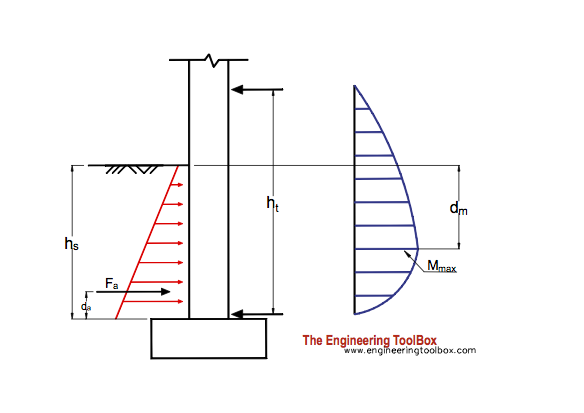
The resultant force due to the earth pressure acting on a basement wall can be calculated as
Fa = 0.5 K γ hs2 (1a)
where
Fa = resultant force acting on the basement wall (kN/m)
hs = height of backfill soil (m)
γ = specific weight of backfill soil (kN/m3)
K = coefficient of earth pressure at rest
Coefficient of earth pressure at rest can be calculated as
K = μ / (1 - μ) (1b)
where
μ = Poisson's ratio
Poisson's ratios for some typical backfill soils:
- clay: 0.41
- sand : 0.29
- sandy clay: 0.37
- sandy loam: 0.31
Specific weight can be calculated as
γ = ρ ag (1c)
where
ρ = density of soil (kg/m3)
ag = acceleration of gravity (9.81 m/s2)
Density for some typical backfill materials:
- clay, dry: 1600 kg/m3
- sand, dry: 1555 kg/m3
The acting position of the acting force can be calculated as
da = hs / 3 (1d)
where
da = distance from the bottom of the basement wall (m)
The maximum bending moment acting in the basement wall can be calculated as
Mmax = (Fa hs / 3 ht) (hs + (2 hs / 3)(hs / (3 ht))1/2) (1e)
where
Mmax = maximum moment in the basement wall (Nm)
The position of the max moment in the basement wall can be calculated as
dm = hs (hs / (3 ht))1/2 (1f)
Note! - cracking of a basement wall is likely to occur where the moment is at the maximum. Due to tension reinforcement bars should be concentrated closer to the inside wall.
1st Floor at Ground Level
The forces that keeps the basement wall in position - the force at the basement floor/slab and the force from the 1. floor joists at ground level - are indicated in the figure below.
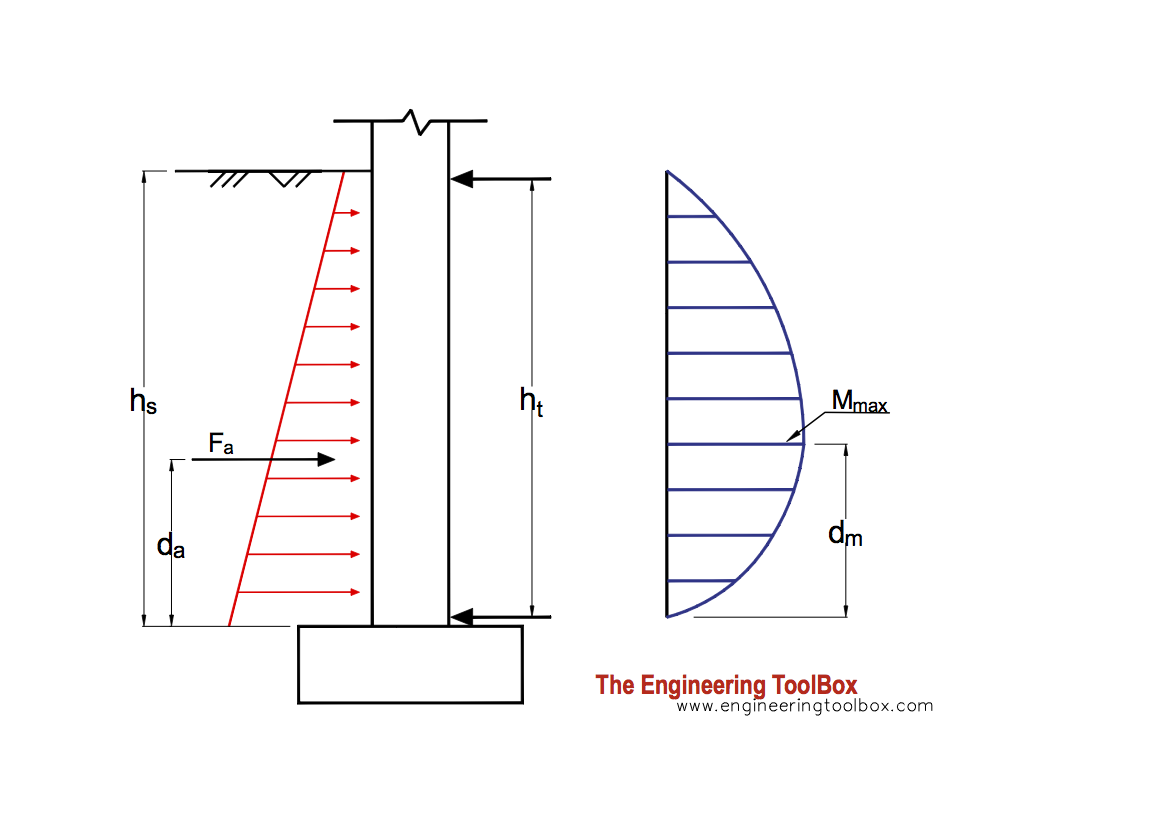
The resultant force due to the earth pressure acting on a basement wall can be calculated as
Fa = 0.5 K γ hs2 (2a)
The acting position of the acting force can be calculated as
da = hs / 3 (2b)
where
da = distance from the bottom of the basement wall (m)
The maximum moment acting in the basement wall can be calculated as
Mmax = 0.128 Fa hs (2c)
where
Mmax = maximum moment in the basement wall (Nm/m)
The position of the max. moment in the basement wall can be calculated as
dm = 0.42 hs (2e)
Example - Earth Pressure on Basement Wall
A basement wall with height 2.5 m is backfilled with sand.
The Poisson's ratio for sand is 0.29 and the coefficient of earth pressure can be calculated as
K = 0.29 / (1 - 0.29)
= 0.41
The specific weight for the sand can be calculated as
γ = (1555 kg/m3) (9.81 m/s2)
= 15255 N/m3
= 15.3 kN/m3
The resultant force acting on the basement wall can be calculated as
Fa = 0.5 (0.41) (15.3 kN/m3) (2.5 m)2
= 19.6 kN/m
The acting position of the resultant force can be calculated as
da = (2.5 m) / 3
= 0.83 m
The maximum moment acting in the basement wall can be calculated as
Mmax = 0.128 (19.6 kN) (2.5 m)
= 6.3 kNm/m
The position of the max. moment in the basement wall can be calculated as
dm = 0.42 (2.5 m)
= 1.05 m



