Law of Sines
Calculate the angles in a generic triangle.
The "Law of Sines" can be used to calculate the angles of a triangle.
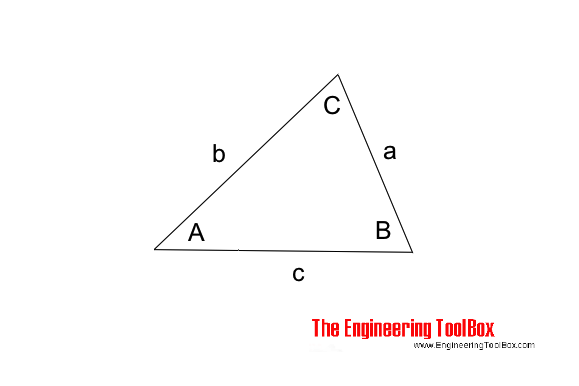
The "Law of Sines" can be expressed as
$$ {a \over sin A } = {b \over sin B } = {c \over sin C } \tag{1}$$
where
a, b and c = length of sides in triangle (m, ft ...)
A, B and C = angles in the triangle (degrees)
Law of Sines Calculator
Eq. 1 can be modified to
$$ a = {b sin A \over sin B } = {c sin A \over sin C } \tag{1a}$$
$$ b = {a sin B \over sin A } = {c sin B \over sin C } \tag{1b}$$
$$ c = {a sin C \over sin A } = {b sin C \over sin B } \tag{1c}$$
This expression can also be handy:
$$ sin \frac{1}{2}A = \sqrt{{(s - b)(s - c) \over b c }} \tag{2}$$
where
$$ s = \frac{1}{2}(a + b + c) \tag{3}$$



