Support Reactions - Equilibrium
Static equilibrium is achieved when the resultant force and resultant moment equals to zero.
Equilibrium of a body requires both a balance of forces to prevent the body from translating or having accelerated motion along a straight or curved path - and a balance of moments to prevent the body from rotating.
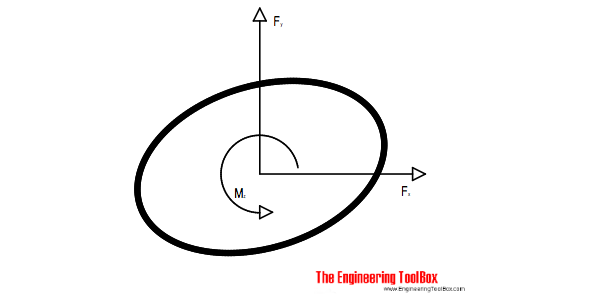
Any static force system will be in equilibrium if the resultant force and resultant moment both are equal to zero.
Static equilibrium in a three dimensional system can be expressed as
Σ F = Σ Fx = Σ Fy = Σ Fz = 0 (1)
Σ M = Σ Mx = Σ My = Σ Mz = 0 (2)
where
F = force (N, lb)
M = moment (Nm, ft lb)
x, y, z = orthogonal axes
Often the loading of a body can be simplified to a two dimensional system with co-planar forces in the x-y plane. Eq. 1 and 2 can be reduced to
Σ F = Σ Fx = Σ Fy = 0 (3)
Σ M = Σ Mz = 0 (4)
The best way to account for all forces acting on a body is to draw the body's free-body diagram . A free-body diagram shows the relative magnitude and direction of all forces acting upon an object in a given situation.
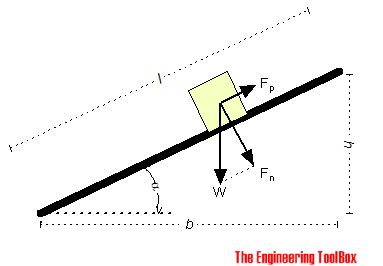
Free-body diagram example - gravity and friction forces acting on a body on an inclined plane
Example - Support Reactions on a Beam with Eccentric Load
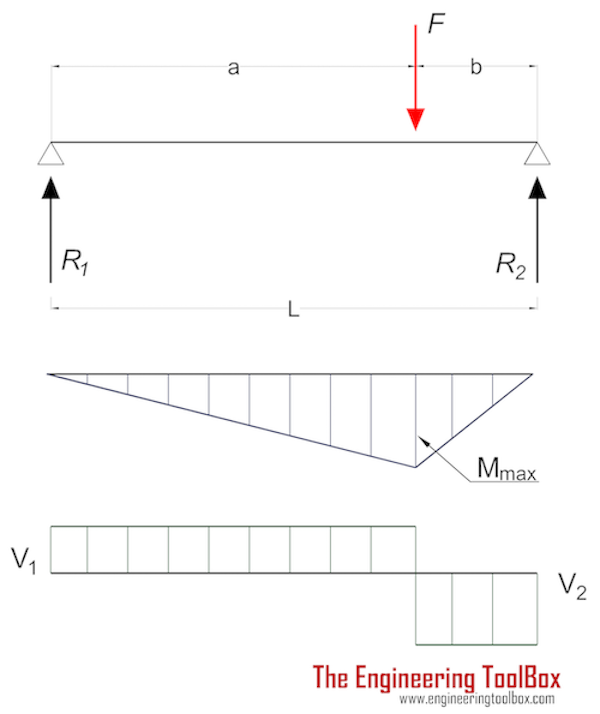
A beam with length 6 m has an eccentric load of 9000 N 4 m from support 1 . Applying the equations of equilibrium we have
Fx = R1x = R2x = 0 (5)
Fy - (R1y + R2y ) = 0 (6)
M1 = Fy a - R2y (a + b) = 0 (7)
Rearranging (7) to express R2y
R2y = F a / (a + b) (7b)
Eq. (7b) with values
R2= (9000 N) (4 m) / ((4 m) + (2 m))
= 6000 N
= 6 kN
Rearranging (6) for R1y
R1y = Fy - R2y (6b)
Eq. (6b) with values
R1y = (9000 N) - (6000 N)
= 3000 N
= 3 kN
Example - Reaction Forces on a Structural Frame
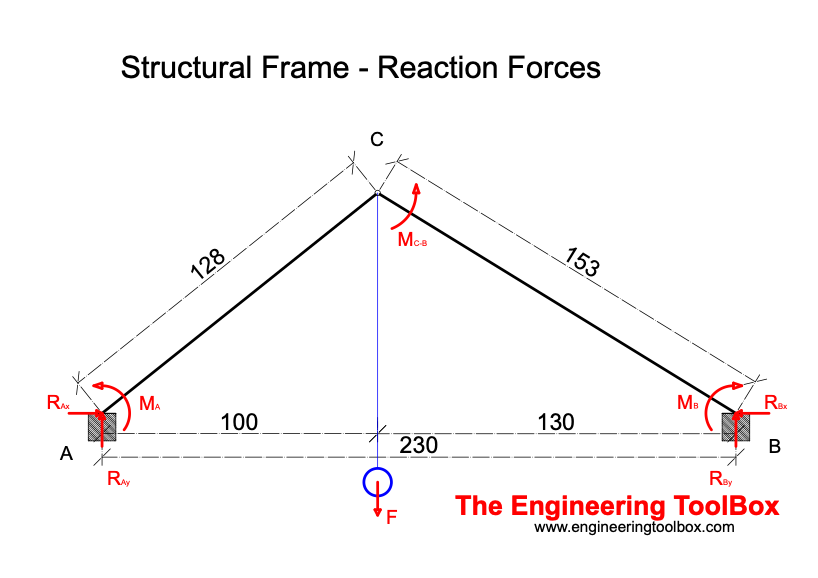
A weight F (1000 N) is hanging in a structural frame as shown in the figure above. A structural analyses can be done with the following equations:
∑MA = RBy (230 cm) - (1000 N) (100 cm)
= 0 (1)
∑MB = RAy (230 cm) - (1000 N) (130 cm)
= 0 (2)
∑MC-B = RBy (130 cm) - RBx h
= 0 (3)
F = RAy + RBy (4)
RAx = RBx (5)
Eq. 1 can be rearranged to
RBy = (1000 N) (100 cm) / (230 cm)
= 435 N
Eq. 2 can be rearranged to
RAy = (1000 N) (130 cm) / (230 cm)
= 565 N
The height h in eq. 3 can be calculated as
h = ((153 cm)2- (130 cm)2)1/2
= 80.7 cm
Eq. 3 can then be rearranged to
RBx = (435 N) (130 cm) / (80.7 cm)
= 700 N
From eq. 5
RAx = RBx
= 700 N



