Satellites in Orbit
Orbital and escape velocity for geostationary satellites.
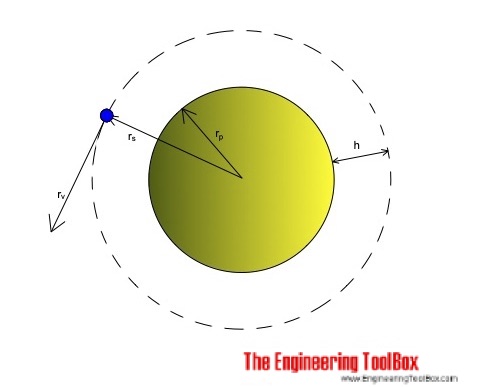
Orbital velocity of a satellite is at maximum at sea level and decreases with height.
Orbital velocity can be calculated as
vs = (g rp2 / rs)1/2 (1)
where
vs = orbital velocity (m/s)
g = acceleration due to gravity (m/s2) (9.81 m/s2)
rp = radius planet (m) (earth: 6.37×106 m)
rs = radius satellite orbit (m)
Maximum velocity at sea level where radius planet equals radius orbit can be expressed as
vs_max = (g rp)1/2 (1b)
Escape velocity where the satellite will leave its orbit and escape the planet gravity can be calculated as
vs_escape = (2 g rp)1/2 (2)
Orbit periodic time can be expressed as
ts = 2 π (rs3 / (g rp2))1/2 (3)
where
ts = orbit time (s)
Height of orbit can be calculated as
hs = rp ((g ts2 / (4 π2 rp))1/3 - 1) (4)
where
hs = height of orbit (m)
Example - Earth bound Satellites
Maximum velocity at sea level:
vs_max = ((9.81 m/s2) (6.37×106 m))1/2
= 7905 m/s
= 7.9 km/h
Escape velocity at sea level:
vs_escape = (2 (9.81 m/s2) (6.37×106 m))1/2
= 11179 m/s
= 11.2 km/h
Height of the synchronous orbit for a geostationary satellite can be calculated by using (4) for an orbit period of 24 hours or 86400 s:
hs = (6.37×106 m) (((9.81 m/s2) (86400 s)2 / (4 π2(6.37×106 m)))1/3 - 1)
= 35968 km



