Process Controllers - P, PI & PID
Proportional, integrating and derivative process controllers.
Basic Controller
The Basic Controller for an application can be visualized as
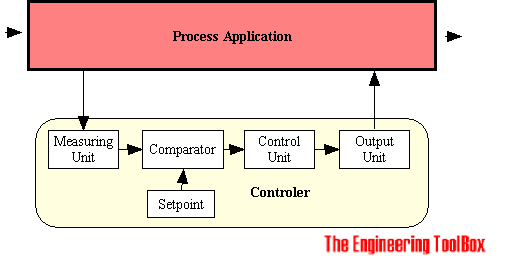
The controller consists of
- a measuring unit with an appropriate instrument to measure the state of process, a temperature transmitter, pressure transmitter or similar
- a input set point device to set the desired value
- a comparator for comparing the measured value with the set point, calculating the difference or error between the two
- a control unit to calculate the output magnitude and direction to compensate the deviation from the desired value
- a output unit converting the output from the controller to physical action, a control valve, a motor or similar
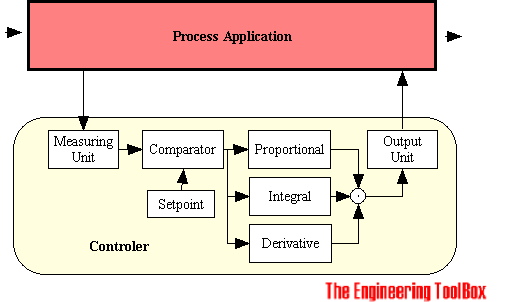
Controller Principles
The Control Units are in general build on the control principles
- proportional controller
- integral controller
- derivative controller
Proportional Controller (P-Controller)
One of the most used controllers is the Proportional Controller (P-Controller) who produce an output action that is proportional to the deviation between the set point and the measured process value.
OP = -kP Er (1)
where
OP = output proportional controller
kP = proportional gain or action factor of the controller
Er = error or deviation between the set point value and the measured value
The gain or action factor - kP
- influence on the output with a magnitude of kP
- determines how fast the system responds. If the value is too large the system will be in danger to oscillate and/or become unstable. If the value is too small the system error or deviation from set point will be very large
- can be regarded linear only for very small variations
The gain kP can be expressed as
kP = 100 / P (1b)
where
P = proportional band
The proportional band P, express the value necessary for 100% controller output. If P = 0, the gain or action factor kP would be infinity - the control action would be ON/OFF.
Note! A proportional controller will have the effect of reducing the rise time and will reduce, but never eliminate, the steady-state error.
Integral Controller (I-Controller)
With integral action, the controller output is proportional to the amount of time the error is present. Integral action eliminates offset.
OI = - kI Σ(Er dt) (2)
where
OI = output integrating controller
kI = integrating gain or action factor of the controller
dt = time sample
The integral controller produce an output proportional to the summarized deviation between the set point and measured value and integrating gain or action factor.
Integral controllers tend to respond slowly at first, but over a long period of time they tend to eliminate errors.
The integral controller eliminates the steady-state error, but may make the transient response worse. The controller may be unstable.
The integral regulator may also cause problems during shutdowns and start up as a result of the integral saturation or wind up effect. An integrating regulator with over time deviation (typical during plant shut downs) will summarize the output to +/- 100%. During start up the output is set to 100%m which may be catastrophic.
Derivative Controller (D-Controller)
With derivative action, the controller output is proportional to the rate of change of the measurement or error. The controller output is calculated by the rate of change of the deviation or error with time.
OD = - kD dEr / dt (3)
where
OD = output derivative controller
kD = derivative gain or action factor of the controller
dEr = deviation change over time sample dt
dt = time sample
The derivative or differential controller is never used alone. With sudden changes in the system the derivative controller will compensate the output fast. The long term effects the controller allow huge steady state errors.
A derivative controller will in general have the effect of increasing the stability of the system, reducing the overshoot, and improving the transient response.
Proportional, Integral, Derivative Controller (PID-Controller)
The functions of the individual proportional, integral and derivative controllers complements each other. If they are combined its possible to make a system that responds quickly to changes (derivative), tracks required positions (proportional), and reduces steady state errors (integral).
Note that these correlations may not be exactly accurate, because P, I and D are dependent of each other. Changing one of these variables can change the effect of the other two.
| Controller Response | Rise Time | Overshoot | Settling Time | Steady State Error |
|---|---|---|---|---|
| P | Decrease | Increase | Small Change | Decrease |
| I | Decrease | Increase | Increase | Eliminate |
| D | Small Change | Decrease | Decrease | Small Change |



