AC - Active, Reactive and Apparent Power
Real, imaginary and apparent power in AC circuits.
The required power supply to an electric circuit depends on the
- active power - real electrical resistance power consumption in circuit
- reactive power - imaginary inductive and capacitive power consumption in circuit
The required power supply is called the apparent power and is a complex value that can be expressed in a Pythagorean triangle relationship as indicated in the figure below.
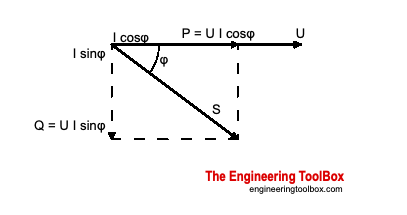
Apparent Power - S
The apparent power is the power supplied to the electric circuit - typical from a power supplier to the grid - to cover the real and reactive power consumption in the loads.
Apparent power can be calculated as
S = (Q2+ P2)1/2 (1)
where
S = apparent power supply to the circuit (volt ampere, VA)
Q = reactive power consumption in load (volt ampere reactive, VAR)
P = active power consumption in load (watts, W)
Apparent power is measured in volt-amperes (VA) - the AC system voltage multiplied with flowing current. Apparent power is a complex value and the vector sum of the active and reactive power as indicated in the figure above.
Single Phase Current
S = U I (2a)
where
U = electric potential (V)
I = current (A)
Three Phase Current
S = 31/2 U I
= 1.732 U I (2b)
Active Power - P
Active - or Real or True - power do the actual work in the load. Active power is measured in watts (W) and is the power consumed by electrical resistance.
- True power is the current in phase (cos(0o) = 1) with the voltage multiplied with the voltage
Single Phase Current
P = U I cos(φ)
= U I PF (3a)
where
φ = phase angle between the electrical potential (voltage) and the current
PF = cos φ
Three Phase Current
P = 31/2 U I cos(φ)
= 1.732 U I PF (3b)
When current and voltage are in phase cos(0o) = 1.
Direct Current
P = U I (3c)
Reactive Power - Q
Reactive power is the imaginary or complex power in a capacitive or inductive load. Reactive power represents an energy exchange between the power source and the reactive loads where no net power is gained or lost. The net average reactive power is zero. Reactive power is stored in and discharged by inductive motors, transformers, solenoids and capacitors. A pure inductor and a pure capacitor do not consume any power since in a half cycle whatever power is received from the source by these components, the same power is returned to the source.
Reactive power should be minimized because it increases the overall current flowing in an electric circuit without providing any work to the load. Increased reactive currents only provides unrecoverable power loss due to power line resistance.
Increased reactive and apparent power will devrease the power factor - PF .
Reactive inductive power is measured in volt-amperes reactive (VAR).
- Reactive power is the current out of phase with the voltage multiplied with the voltage
Single Phase Current
Q = U I sin(φ) (4a)
where
φ = phase angle
Three Phase Current
Q = 31/2 U I sin(φ)
= 1.732 UI sin(φ) (4b)
When current and voltage are in phase sin(0o) = 0.



