Liquid Flow from Containers - Emptying Time
Calculate liquid velocity, volume flow and draining time when emptying a container.
Base Apertures
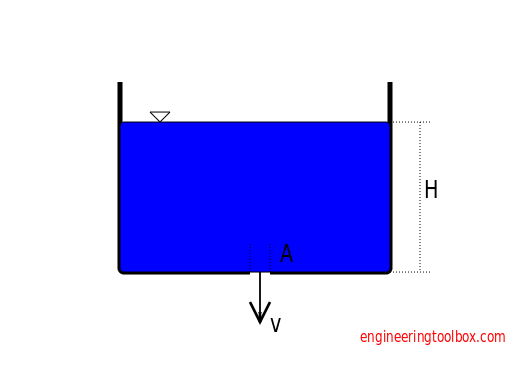
The liquid outlet velocity when draining a tank or a container can be calculated
v = Cv (2 g H)1/2 (1a)
where
v = outlet velocity (m/s)
Cv = velocity coefficient (water 0.97)
g = acceleration of gravity (9.81 m/s2)
H = height (m)
The liquid volume flow can be calculated
V = Cd A (2 g H)1/2 (1b)
where
V = volume flow (m3/s)
A = area of aperture - flow outlet (m2)
Cd = discharge coefficient
where
Cd = Cc Cv
where
Cc = contraction coefficient (sharp edge aperture 0.62, well rounded aperture 0.97)
A = area aperture (m2)
Example - Volume Flow when draining a Container
The height from the surface to the outlet aperture in a water filled container is 3 m. The aperture is sharp edged with diameter 0.1 m. The discharge coefficient can be calculated as
Cd = 0.62 0.97
= 0.6
The area of the aperture can be calculated as
A = π ((0.1 m) / 2)2
= 0.008 m2
The volume flow through the aperture can be calculated as
V = 0.6 (0.008 m2) (2 (9.81 m/s2) (3 m))1/2
= 0.037 m3/s
For height 1.5 m the volume flow is 0.026 m3/s. For height 0.5 m the volume flow is 0.015 m3/s.
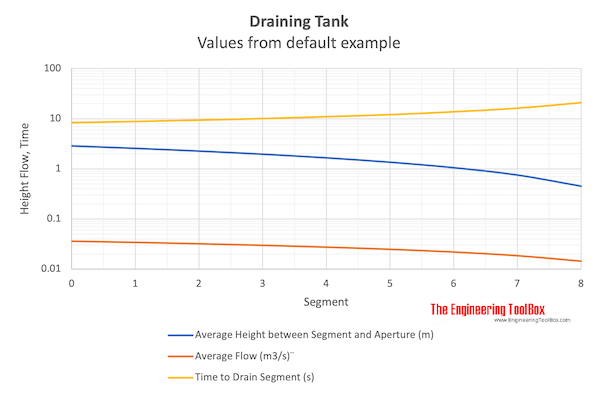
Draining Tank Calculator
This calculator is based on eq. (1b) and can be used to estimate the volume flow and time used to drain a container or tank through an aperture.
The calculator divides the container in "slices" and makes an iterative average calculation for each slice. The accuracy of the calculation can be increased by increasing the number of slices.
- results in table below!
Note! - the flow is reduced and the time is increased with reduced height.
Small Lateral Apertures
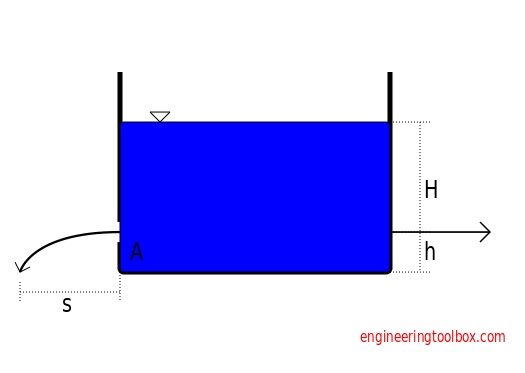
Outlet velocity can be expressed as
v = Cv (2 g H)1/2 (2a)
Distance s can be expressed as
s = 2 (H h)1/2 (2b)
Volume flow can be expressed as
V = Cd A (2 g H)1/2 (2c)
Reaction force can be expressed as
F = ρ V v (2d)
where
ρ = density (kg/m3) (water 1000 kg/m3)
Large Lateral Apertures
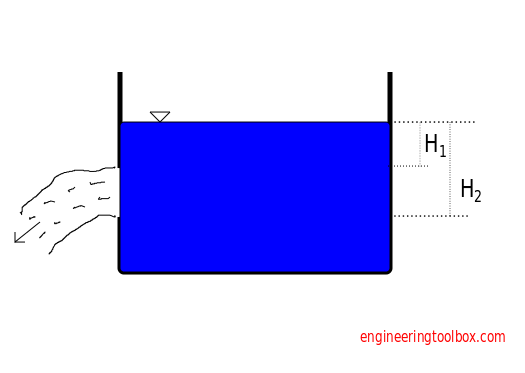
Volume flow can be expressed as
V = 2/3 Cd b (2 g)1/2 (H23/2 - H13/2) (3a)
where
b = width of aperture (m)
Excess Pressure in Container
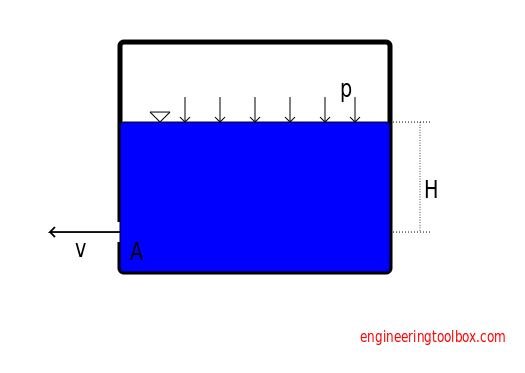
Outlet velocity can be expressed as
v = Cv (2 (g H + p / ρ))1/2 (4a)
where
p = excess pressure in container or tank (N/m2, Pa)
Volume flow can be expressed as
V = Cd A (2 (g H + p / ρ))1/2 (4b)