Sound Propagation - the Inverse Square Law

In a free field - a doubling of the distance from a noise source reduces the sound pressure level with 6 decibel.

This - the Inverse Square Law - can be expressed in a diagram like

Download and print the Inverse Square Law chart - Sound pressure level reduction vs. distance from source

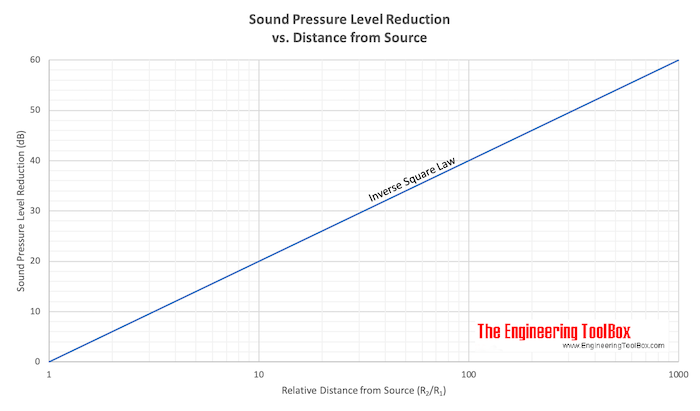
dL = L_p2 - L_p1

     = 10 log(R₂ / R₁)²

     =  20 log(R₂ / R₁)                                        (1)

where

dL = difference in sound pressure level (dB)

L_p1 = sound pressure level at location 1 (dB)

L_p2 = sound pressure level at location 2 (dB)

R₁ = distance from source to location 1 (ft, m)

R₂ = distance from source to location 2 (ft, m)

A "free field" is defined as a flat surface without obstructions.

Example - Rifle Shot and Sound Pressure at Distance

If the sound pressure from a rifle shot is measured to 134 dB at 1.25 feet - the reduction in sound pressure level at distance 80 feet can be calculated as

dL = 20 log((80 ft) / (1.25 ft))

     = 36 dB 

The sound pressure level at distance 80 ft can be calculated as

 L_p2 = (134 dB) - (36 dB)

       = 98 dB

Inverse Square Law Calculator

Use the calculator below to calculate the sound pressure level at distance.

L_p1 - sound pressure level at location 1 (dB)

R₁ - distance from source to location 1 (m, ft)

R₂ - distance from source to location 2 (m, ft)

Example - Noise from a Machine

The noise from a machine in distance 1 m is measured to 110 dB. The noise reduction due to the inverse square law to a working area at distance 5 m can be calculated as

dL = 20 log((5 m) / (1 m))

     = 14 dB 

The sound pressure level in the working area can be calculated as

 L_p2 = (110 dB) - (14 dB)

       = 96 dB

This noise level is only permitted for a limited amount of time and some action with partial barriers or enclosure of the machine should be done.