Buffer Solutions

A buffer solution is a solution that resists a change in pH when small quantities of either H ⁺ ions (an acid) or OH ^- ions (a base) are added. By choosing the right components, a solution can be buffered to almost any pH.

A buffered solution may contain a weak acid and its salt (HA + MA, where M is the salt kation) or a weak base and its salt (B + BHN), where N is the salt anion)

• Buffer solutions achieve their resistance to pH change because of the presence of an equilibrium between the acid HA and its conjugate base A ⁻ .

  HA ⇌ H ⁺ + A ⁻ (Eq. I)

• Buffered solutions contain relatively large concentrations of a weak acid and its corresponding weak base. They can involve a weak acid HA and a conjugate base A ^- or a weak base B and the conjugate acid BH ⁺ .

• When H+ is added to a buffered solution, it reacts essentially to completion with the weak base present:

H ⁺ + A ^- →  HA       or      H ⁺ +  B  →  BH ⁺

• When OH- is added to a buffered solution, it reacts essentially to completion with the weak acid present:

OH ^- + HA  →  A ^- + H₂O         or       OH ^- +  BH ⁺ →  B  +  H₂O

• The pH of the buffered solution is determined by the ratio of the concentrations of the weak base and weak acid. As long as this ratio remains virtually constant, the pH will remain constant. This will be the case as long as the concentrations of the buffering material  (HA and A ^- ) or (B and BH ⁺ ) are large compared with the amounts of H ⁺ or OH ^- added.

For an acidic solution (without salt) we have an equilibrium constant, K _a :

K _a = [H ⁺ ] [A ^- ]/[HA]

and we can assume that the concentrations [H ⁺ ] and [A ^- ] are the same, and much smaller than [HA] if the acid is weak. We can assume that so little of the acid has ionised that the concentration of the acid [HA] at equilibrium is the same as the concentration of the acid we used.

This is not true anymore when we add the corresponding salt (MA), containing A ^- and M ⁺ ions. Then Eq. I will be pushed further to the left according to Le Chatelier's Principle for solutions at equilibrium. Then we can assume that the number of [A ^- ] present in the solution is the same as coming from the salt MA. The concentration of the acid [HA], can still be assumed to be the same as the concentration of the acid we used, now that the equilibrium has been moved even further to the left. (Due to lack of H ⁺ ions it will not be higher than what we started with).

The buffer capasity of a buffered solution is defined in terms of the amount of protons or hydroxide ions it can adsorb without a significant change in pH. Thus, a solution with a high concentration of the buffering compounds, will have a high buffer capasity.

• The pH of a buffering solution is determined by the [A-]/[HA] ratio
• The buffer capasity is depenent on the magnitude of  [A-] and [HA] .

For solutions with known concentrations of the acid and the conjugate base, you can calculate the pH by use of the Henderson-Hasselbalch equation , which is on the log form:

pH = pK _a + log ([A ^- ]/[HA])  =  pK _a +  log ([base]/[acid])

• The best buffering effect is achieved when the [A ^- ]/[HA] ratio is 1. Then the acid have a pK _a equal to pH. This means that we should aim for a buffering acid or base with a pK _a value closest possible to the wanted pH.

Examples given for better understanding and help in calculations:

1. To calculate the pH of a given buffer solution
2. To make a buffer solution with a wanted pH
3. To make a buffer solution with pH above 7
4. How to make 1.4 liter 1 M (mol/l solution) ammonium chloride water solution
5. How to make 1.0 liter 1 M ammonia water solution
6. Differences in buffer capacity
7. To choose the best buffer solution

See also pKa of phenols, alcohols and carboxylic acids , pKa of amines, diamines and cyclic organic nitrogen compounds and pKa of inorganic acids and bases as well as Strong and weak acids and bases .

Example 1: To calculate the pH of a given buffer solution

A buffer solution is made from equal amounts of 0.40 M CH₃ COOH (ethanoic acid) and 0.25 M NaCH₃ COO (sodium ethanoate).  What will be the pH of this solution?

(M = mol/ liter solution)

pKa for ethanoic acid is 4.76, which gives K _a = 10 ^(-4.76) = 1.74*10 ^-5

K _a = [H ⁺ ] [CH₃ COO ^- ]/[CH₃ COOH]   and   [H ⁺ ] = K _a [CH₃ COOH]/[CH₃ COO ^- ]

[H ⁺ ] = 1.74*10 ^-5 *0.40/0.25 = 2.78*10 ^-5

pH = -log[H+] = -log (2.78*10 ^-5 ) = 4.56 = 4.6 (only two significant figures due to the numbers of significant figures in the input values)

Or by use of Henderson-Hasselbalch equation : pH = 4.76 + log(0.25/0.40) = 4.76 -0.20 = 4.56 = 4.6

Example 2: To make a buffer solution with a wanted pH

How much of CH₃ COOH (ethanoic acid) and NaCH₃ COO (sodium ethanoate) do we need to make a buffer solution with pH of 3.95?

The acid equilibrium equation:

CH₃ COOH( aq )   ↔    H ⁺ ( aq ) +  CH₃ COO ^- ( aq )

K _a = [H ⁺ ] [CH₃ COO ^- ]/[CH₃ COOH]     and    [CH₃ COO ^- ]/[CH₃ COOH] = K _a /[H ⁺ ]

pH = 3.95 corresponds to a concentration [H+] = 10 ^(-3.95) = 1.12*10^-4

pKa for ethanoic acid is 4.76, which gives K _a = 10 ^(-4.76) = 1.74*10 ^-5

Then, [CH₃ COO ^- ]/[CH₃ COOH] = 1.74*10 ^-5 /1.12*10^-4 = 0.16

This means that the concentration of the sodium salt should be 0.16 times of the concentration of the ethanoic acid.

If you start with 1.0 liter of 1 M ethanoic acid, you can add 1 liter of 0.16 M sodium ethanoate. (M = mol/ liter solution)

The figure shows the changes in pH for the buffer solution with addition of HCl:

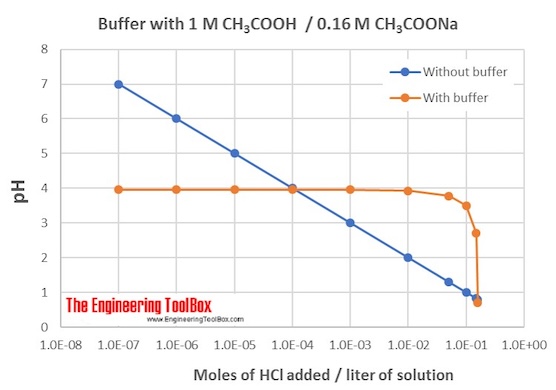
Note 1: This can be solved with a number of different concentrations of the two solutions. However, the amounts must be adjusted so that the ratio between the added CH₃ COO ^- and CH₃ COOH remains 0.16 in the blend.

Note 2: When the amount of CH3COO ^- is relatively small compared to the amount of CH3COOH, as in this case, the buffering effect will be smaller than when the amounts of the two are more equal. To compensate for this, you can increase the concentration of both (still with the same ratio between them) or find another pair of acid and salt with a pK _a closer to the pH you want. (E.g. formic acid (HCOOH) with pKa = 3.74 and the salt sodium formate (HCOONa))

Example 3: To make a buffer solution with pH above 7

How can we make an alkalic buffer solution, e.g.  with pH = 9.1?

With a pH of 9.1 we will be on the basic side, with OH- ions dominating over H+ ions. Then, you should find a base and its salt to produce the buffer from, e.g. the base ammonia (NH3) and its salt ammonium chloride (NH4Cl).

The equilibrium equation will be:

NH₃ ( aq )  + H₂O( l )  ↔ NH ₄ ⁺ ( aq )  +  OH ^- ( aq )

K _b = [OH ^- ] [NH ₄ ⁺ ]/[NH₃ ]   and   [NH ₄ ⁺ ]/[NH₃ ] = K _b /[OH ^- ]

For ammonia, the pK _a = 9.24.    Then, pK _b = 14 - pK _a = 14 -9.24 = 4.76     and K _b = 10 ^(-4.76) = 1.74*10 ^-5

We also have: pH +pOH = 14   and  pOH = 14 - pH = 14 - 9.1 = 4.9     [OH-] = 10 ^(-4.9) = 1.26* 10 ^-5

We fill in the equation for K _b and [OH ^- ]: [NH ₄ ⁺ ]/[NH₃ ] = K _b /[OH ^- ]  = 1.74*10 ^-5 /1.26* 10 ^-5 = 1.38

To make a buffer with pH = 9.1 you may start with 1.4  liter of 1 M ammonium chloride water solution and add 1.0 liter of 1 M ammonia water  solution. (M = mol/ liter solution)

Note : This can be solved with a number of different concentrations of the two solutions. However, the amounts must be adjusted so that the [NH ₄ ⁺ ]/[NH₃ ] ratio for added chemicals remains 1.38.

Exemple 4: How to make 1.4 liter 1 M (mol/l solution) ammonium chloride water solution?

Molweight of ammonium chloride, NH ₄ Cl:

1 mol N: 14.01 g/mol,     1 mol H: 1.01 g/mol,      1 mol Cl: 35.45 g/mol

1 mol NH ₄ Cl: (14.01 + 4*1.01 + 35.45) g/mol = 53.50 g NH ₄ Cl/mol

For 1.4 liter we need: 1 mol/l *53.5 g NH ₄ Cl/mol * 1.4 l = 74.9 g NH ₄ Cl

So: Add 74,9 g NH ₄ Cl to a bottle and add approximately 1 liter of water. Stirr untill all the salt is solved. Add more water to accurate 1.4 liter solution.

Example 5: How to make 1.0 liter 1 M ammonia water solution?

Ammonia is a gas at room temperature, however it is also available as liquid solved in water, typically 30 % by weight ammonia in water.

For 1.0 liter of a 1 M solution we need 1 mol NH _3. 1 mol NH₃ : (14.01 + 3*1.01) g/mol = 17.04 g NH₃ /mol

100 g of 30 weight% ammonia solution contains 30 g ammonia.  We need: (100g solution/30g ammonia)* 17.04 g ammonia = 56.80 g 30weight% solution.

So: Add 56.8 g 30 weight% NH₃ -solution  to a bottle and add water to a total of 1 liter.

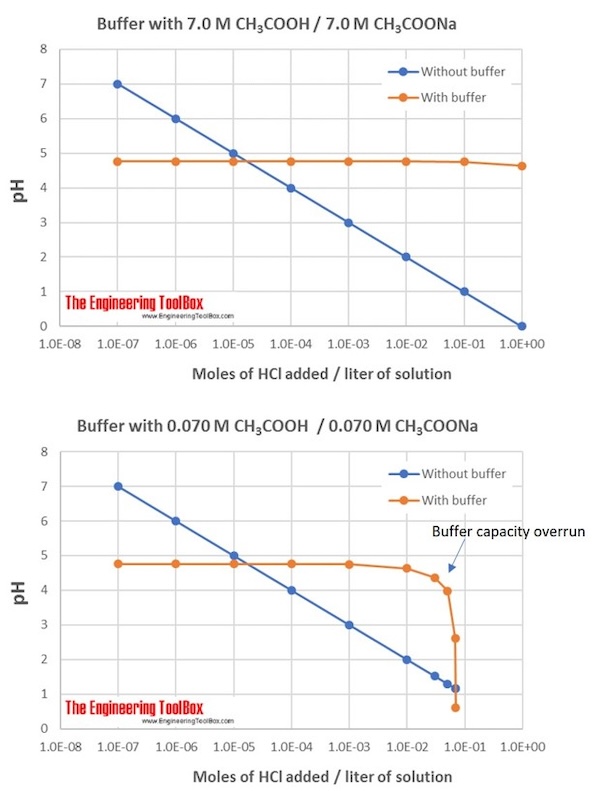
Example 6: Differences in buffer capacity

What will the change in pH be when 0.20 mol gaseous HCl is added to 0.5 liter of each of the two solutions given below?

1. 7.00 M CH₃ COOH and 7.00 M CH₃ COONa

2. 0.070 M CH₃ COOH and 0.070 M CH₃ COONa

(M = mol/liter solution)

pK _a for ethanoic acid, (CH₃ COOH) , is 4.76, which gives K _a = 10 ^(-4.76) = 1.74*10 ^-5

From the Henderson-Hasselbalch equation: pH = pK _a + log ([A ^- ]/[HA])

Solution 1: pH = 4.76 +  log ([7.00]/[7.00]) = 4.76 + log (1) = 4.76 + 0 = 4.76

Solution 2: pH = 4.76 +  log ([0.070]/[0.070]) = 4.76 + log (1) = 4.76 + 0 = 4.76

The species present in the solutions after addition of HCl gas:

H2O     CH3COOH     CH3COO ^- Na ⁺ H ⁺ Cl ^-

The Na ⁺ and Cl ^- ions will not be part of any reaction, but when HCl is added, the amount of H ⁺ is increased, and the equlibrium

CH₃ COOH(aq)   ↔    H ⁺ (aq) +  CH₃ COO ^- (aq)

is driven to the left. All the added H ⁺ (0.01 mol) will be reacted with CH₃ COO ^- to CH₃ COOH.

The concentrations of the acid compounds in Solution 1 before and after reaction will be:

Concentrations of Acid Compounds Solution 1

	[H + ]	[CH3 COO - ]	[CH3 COOH]
Before reaction	0.010 mol/0.5 l = 0.020 M	7.00 M	7.00 M
After reaction	0	6.98 M	7.02 M

Then, the pH after reaction can be calculated:

pH of solution 1 after addition of HCl = 4.76 +  log ([6.98]/[7.02]) = 4.76 - 0.0025 = 4.76,   no significant change in pH

The concentrations of the acid compounds in Solution 2 before and after reaction will be:

Concentrations of Acid Compounds Solution 2

	[H + ]	[CH3 COO - ]	[CH3 COOH]
Before reaction	0.010 mol/0.5 l = 0.020 M	0.070 M	0.070 M
After reaction	0	0.050 M	0.090 M

Then, the pH after reaction can be calculated:

pH of solution 2 after addition of HCl = 4.76 +  log ([0.050]/[0.090]) = 4.76 - 0.26 = 4.50,     a small, but significant, change in pH.

Solution 1 has a much higher buffer capacity than Solution 2.

The figure shows the differences in buffer capacity for the two solutions:

Example 7: To choose the best buffer solution

You need a buffer with pH 4.5 and have four acids and their sodium salt availible. Which acid should you use to get the best buffer solution?

Your acids:

• Chloroacetic acid
• Benzoic acid
• Propanoic acid
• Hypochlorous acid

We know that the best buffering effect is achieved when the buffering weak acid or base have a pK _a value close to the wanted pH.

So, we need to compare the acids pK _a s to the wanted pH of 4.5.  If we take a look at pK _a of inorganic acids and pk _a of phenols, alcohols and carboxylic acids we find the pK _a s of the acids:

Chloroacetic acid:   2.87
Benzoic acid:          4.20
Propanoic acid:      4.87
Hypochlorous acid: 7.54

Both benzoic and propanoic acids could be used, but the pK _a of benzoic acid (4.20) is closest to the pH of 4.5 , so benzoic acid and the salt sodiumbenzoate will give the most efficient buffer solution.

Then, the acid equilibrium equation:

C₆ H₅ COOH( aq )   ↔    H ⁺ ( aq ) +  C₆ H₅ COO ^- ( aq )

K _a = [H ⁺ ] [C₆ H₅ COO ^- ]/[C₆ H₅ COOH]     and    [C₆ H₅ COO ^- ]/[C₆ H₅ COOH] = K _a /[H ⁺ ]

pH = 4.50 corresponds to a concentration [H ⁺ ] = 10 ^(-4.50) = 3.16*10 ^-5

pKa for benzoic acid is 4.20, which gives K _a = 10 ^(-4.20) = 6.31*10 ^-5

Then, [C₆ H₅ COO ^- ]/[C₆ H₅ COOH] = 6.31*10 ^-5 /3.16*10 ^-5 = 2.0

This means that the concentration of the sodium salt must be 2 times of the concentration of the benzoic acid.

If you start with 1.0 liter of 1.0 M bencoic acid, you can add 1.0 liter of 2.0 M sodium benzoate. (M = mol/ liter solution)

Temperature ^oC
K
^oF

Length m
km
in
ft
yards
miles
naut miles

Area m²
km²
in²
ft²
miles²
acres

Volume m³
liters
in³
ft³
us gal

Weight kg_f
N
lbf

Velocity m/s
km/h
ft/min
ft/s
mph
knots

Pressure Pa
bar
mm H₂O
kg/cm²
psi
inches H₂O

Flow m³/s
m³/h
US gpm
cfm